Information geometric regularization
The first inviscid regularization of high-speed gas dynamics
The problem: Shock formation in gas dynamics
This post summarizes joint work with Ruijia Cao on a new approach for handling shocks in compressible fluid mechanics.
Shock formation
The density and velocity profiles of compressible and (nearly) inviscid gases steepen over time, as faster gas particles catch up to slower ones. Eventually, the profiles become almost discontinuous. These shock waves are crucial phenomena in many domains, such as astrophysics and aerospace applications.

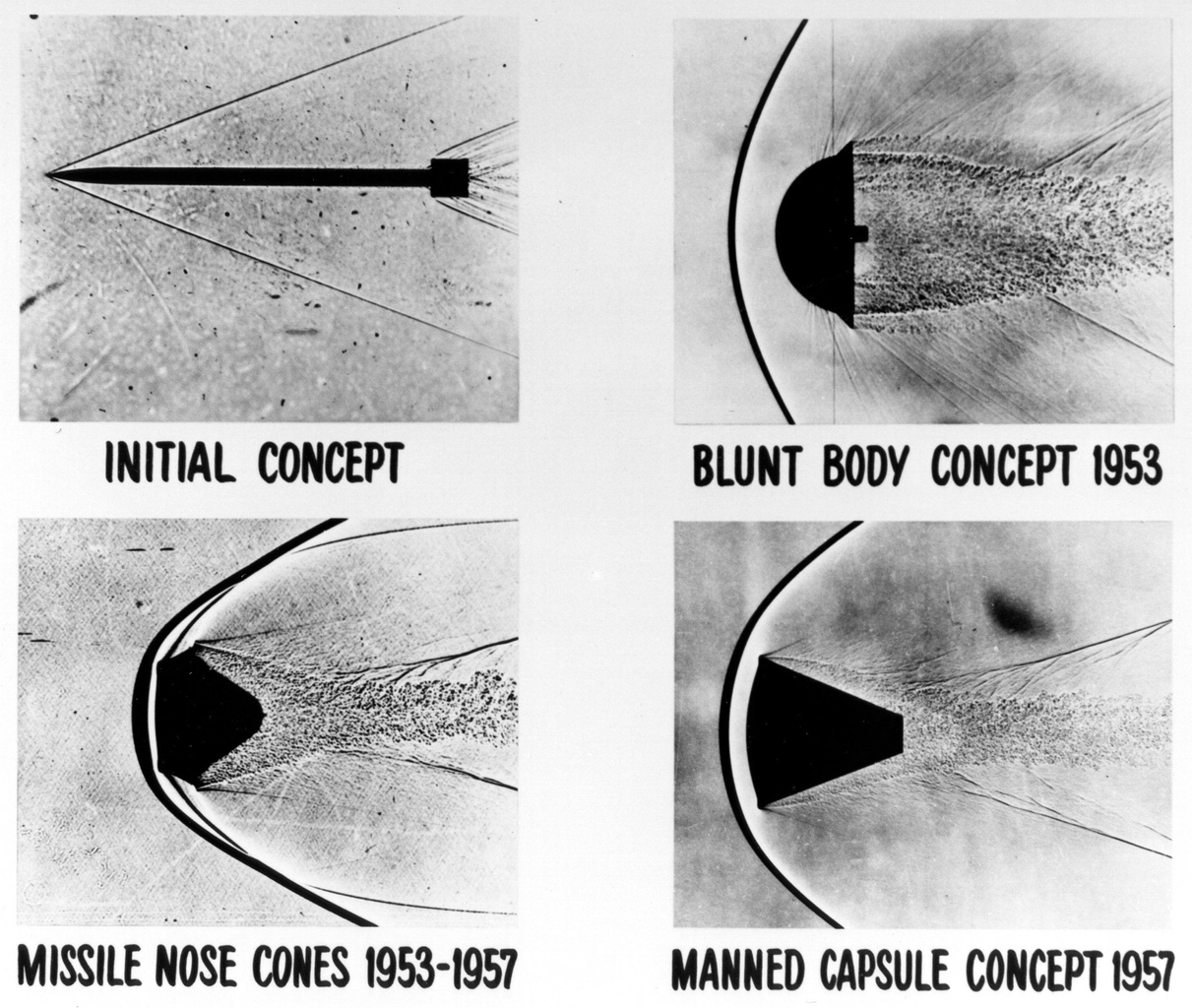
Shocks— a multiscale problem
Shock waves appear discontinuous on macroscopic scales. But on sufficiently small scales the viscosity of the gas preserves their smoothness. This usually happens on the scale of the mean free path length — the average distance that gas particles travel between collisions. In atmosspheric conditions, this distance is on the order of microns, vastly smaller than the scales relevant to aerospatial simulations and impossible to resolve in numerical simulations.
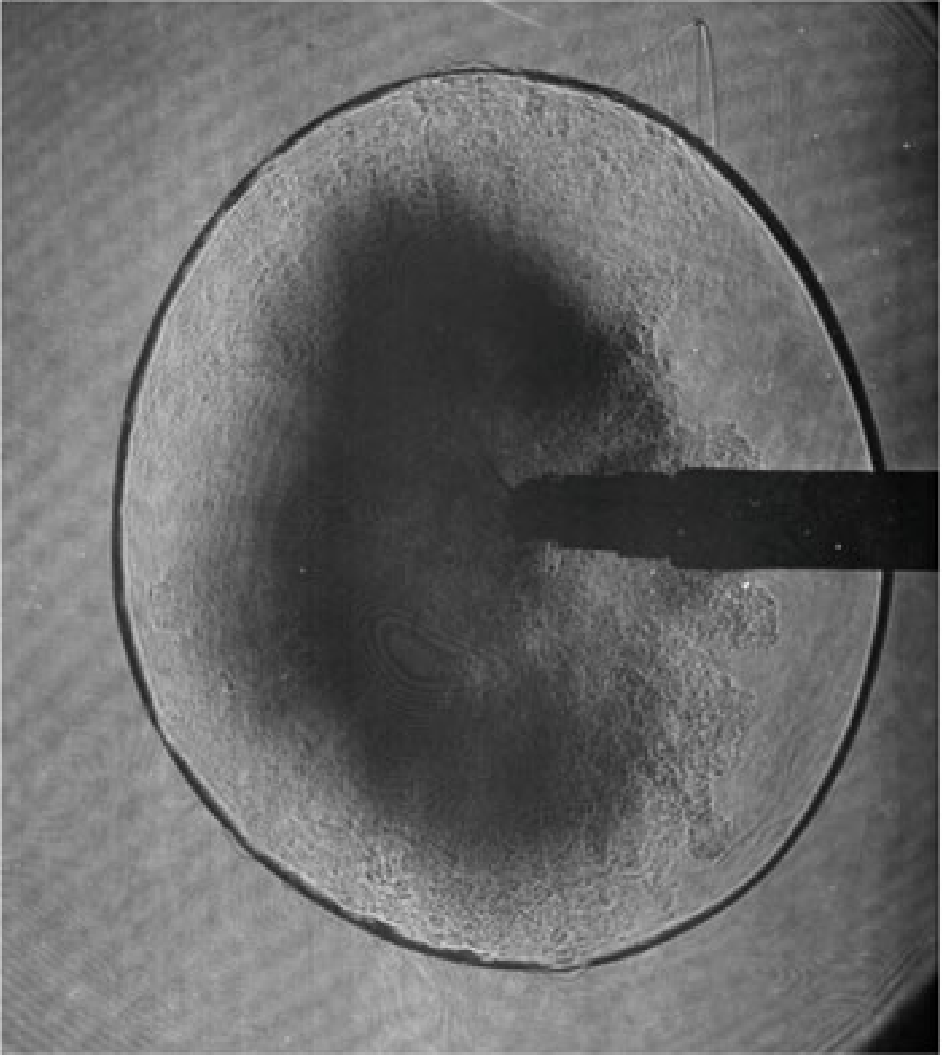
Numerical challenges due to shocks
Most numerical methods use smooth functions, such as polynomial, trigonometric, neural network, or radial basis functions, to approximate the solution. If the solution is discontinuous, the Gibbs-Runge oscillations can cause the simulation to break down. Artifically adding viscosity avoids oscillations but introduces excessive energy dissipation.
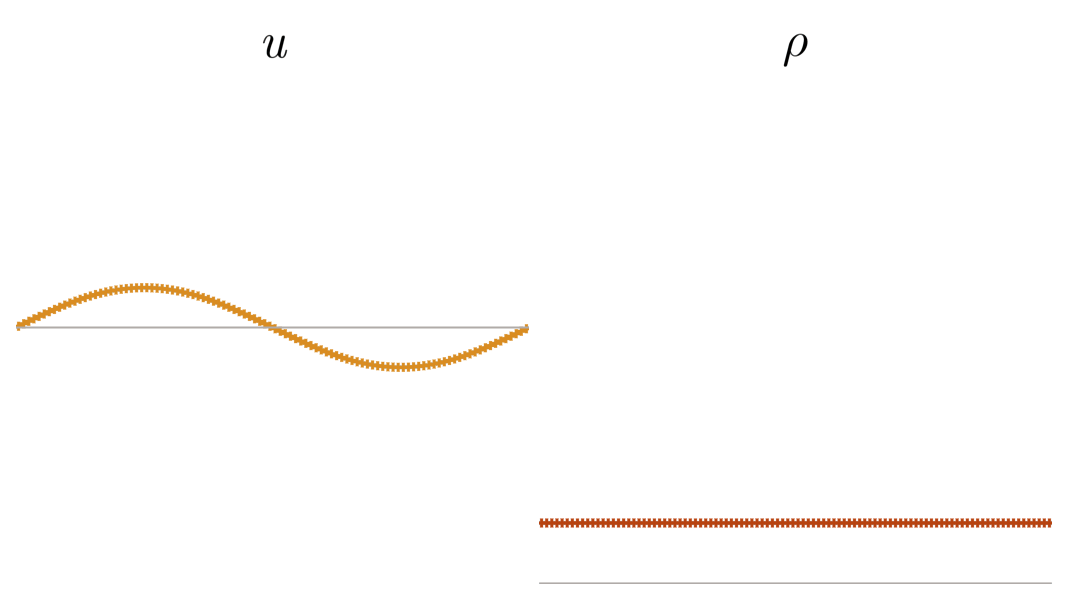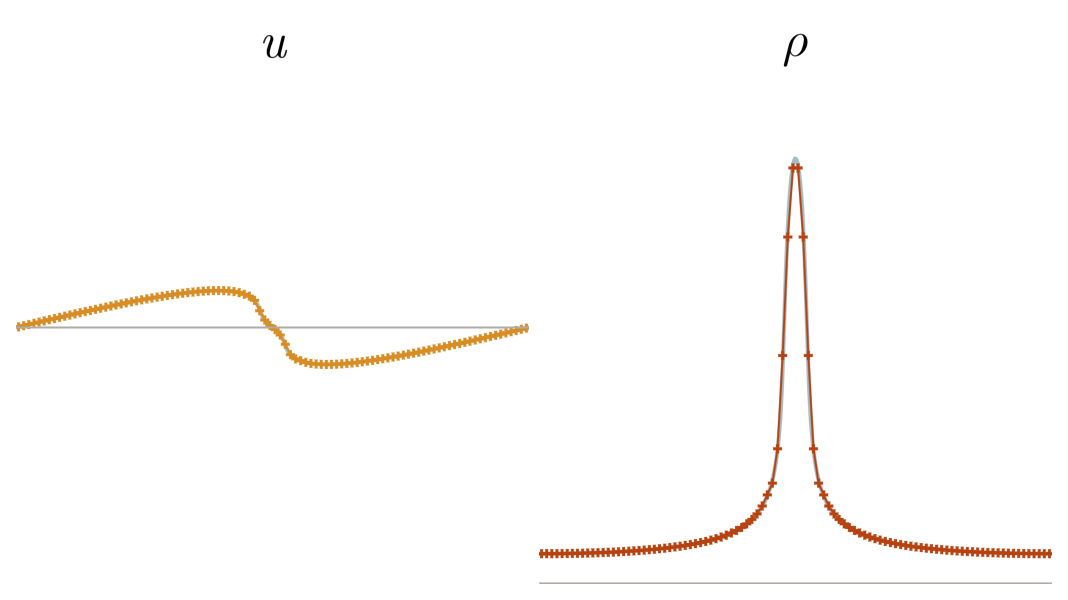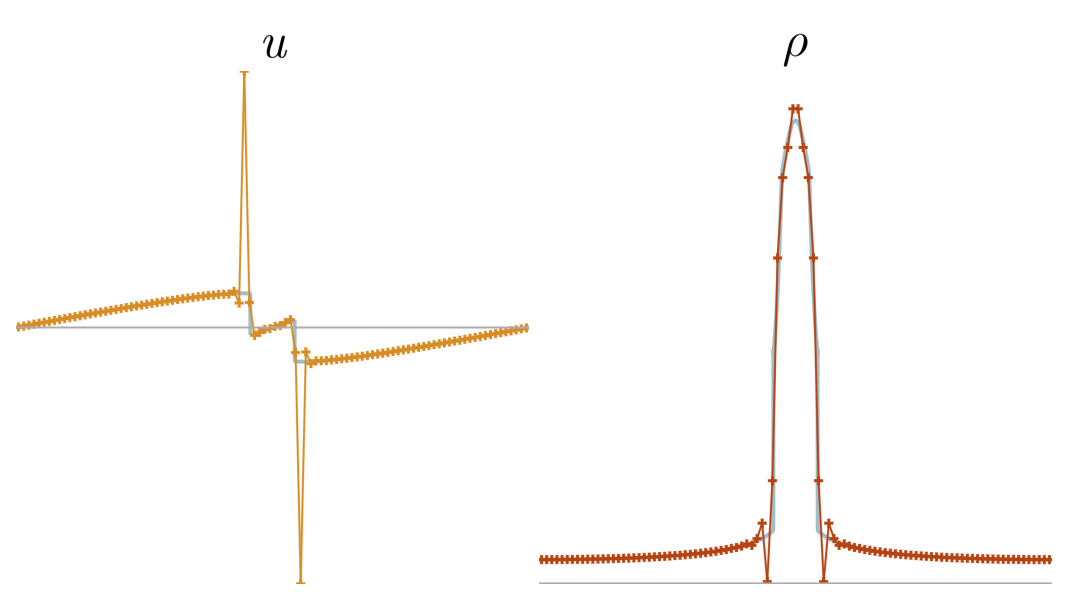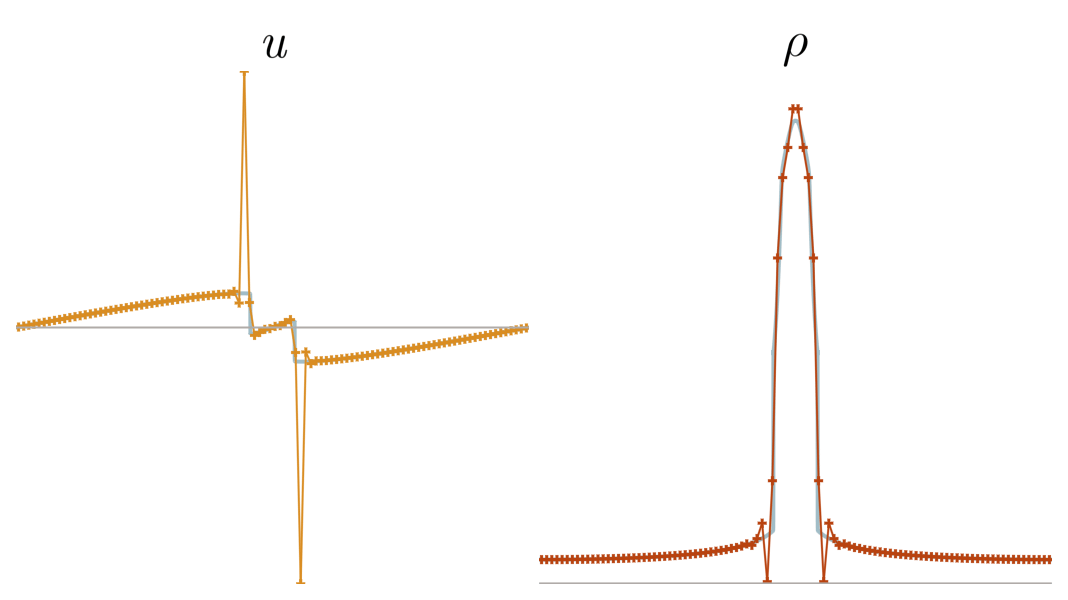
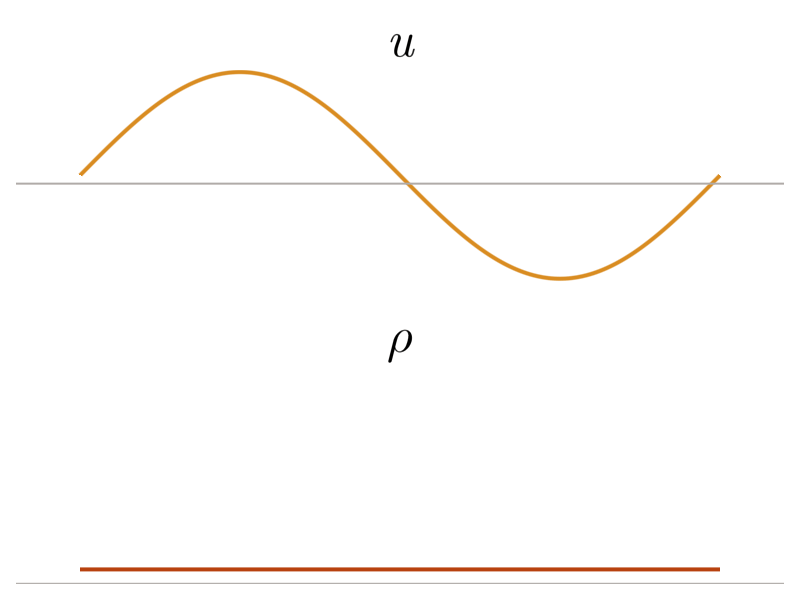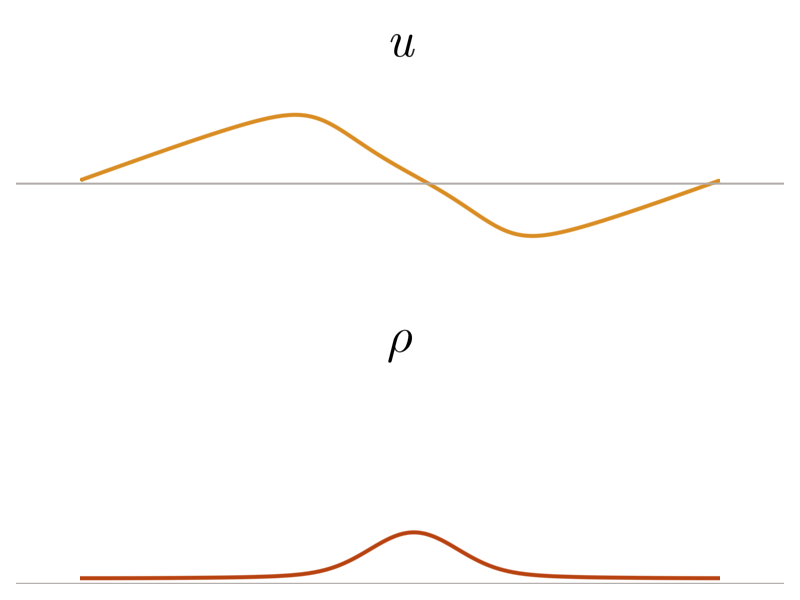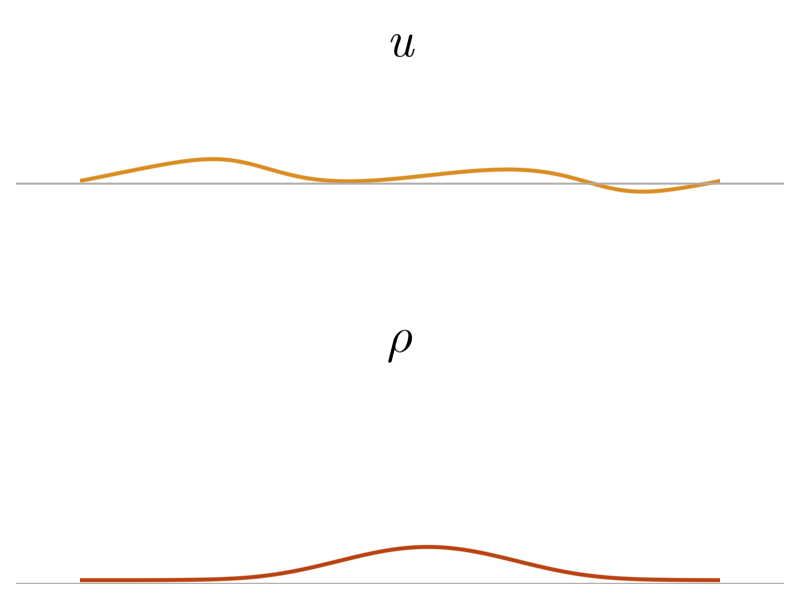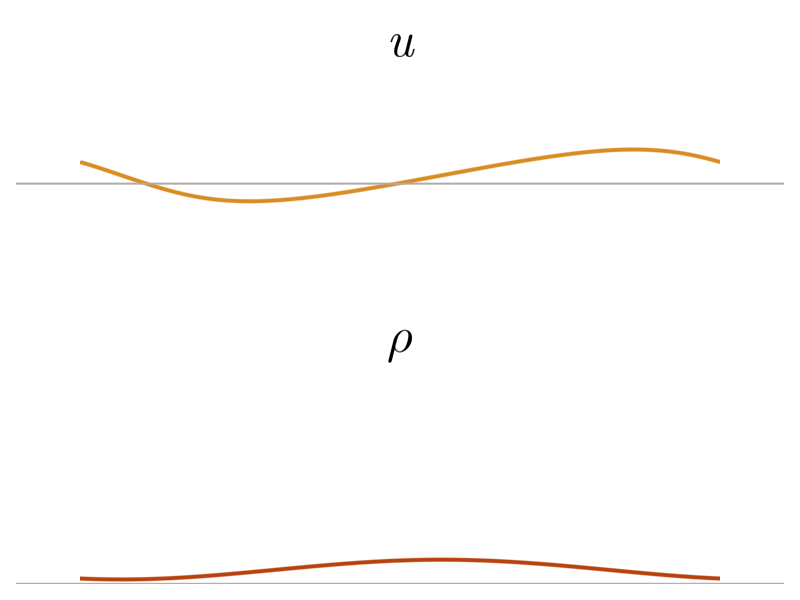
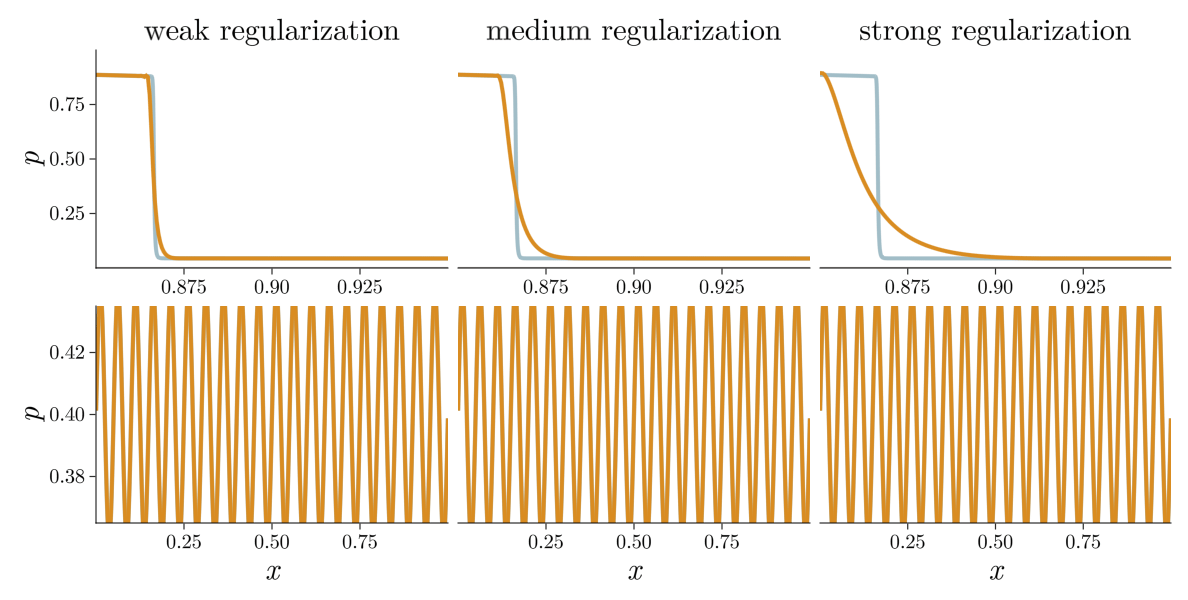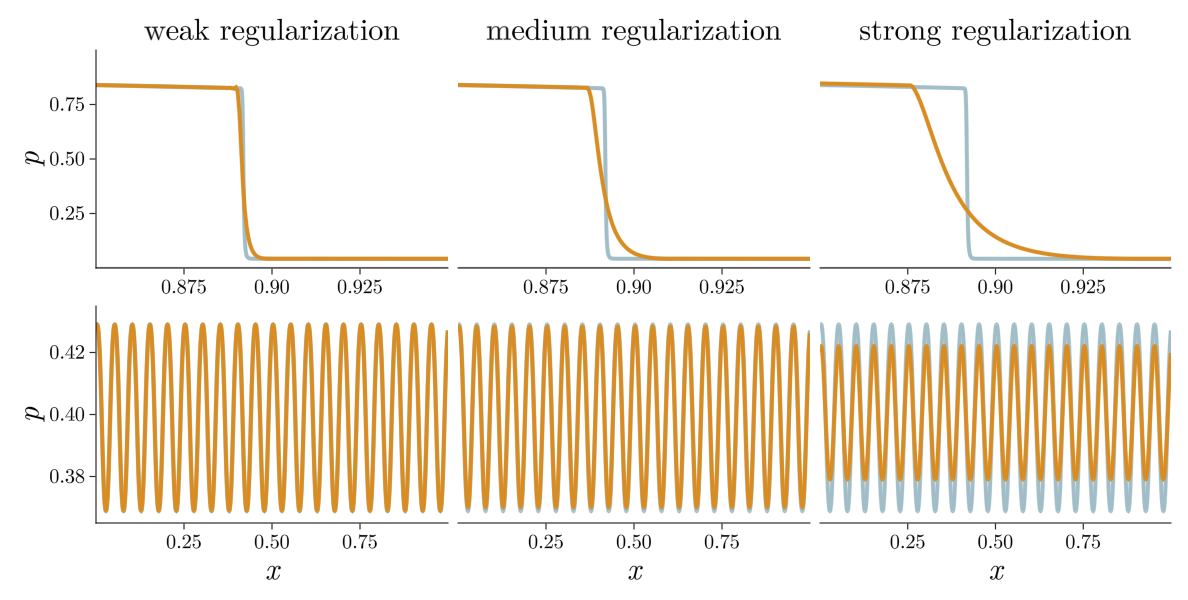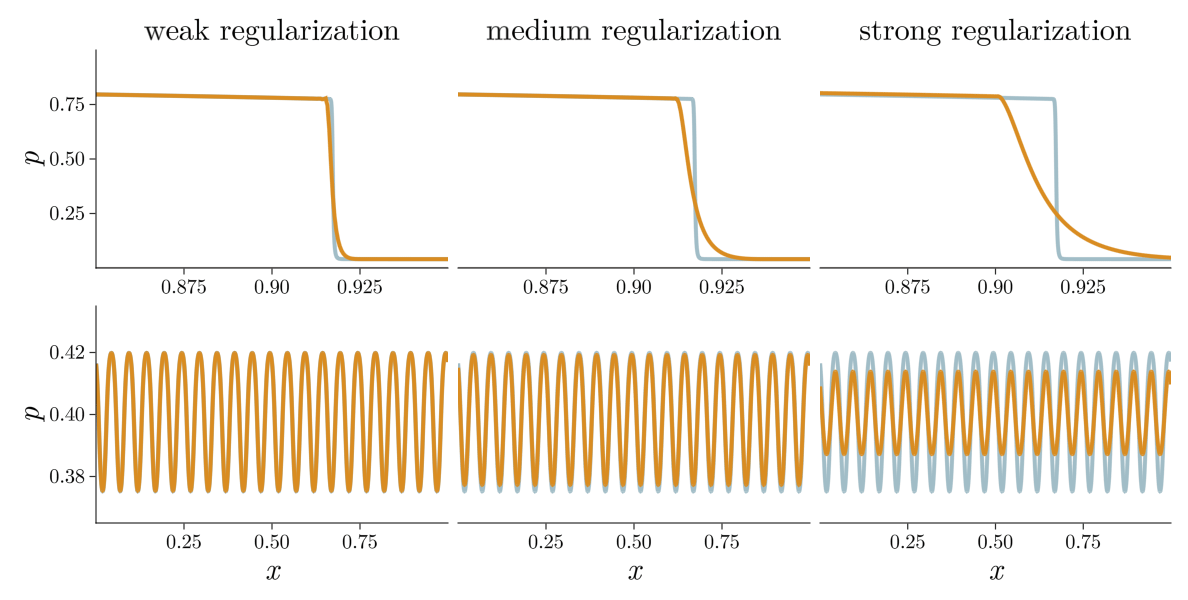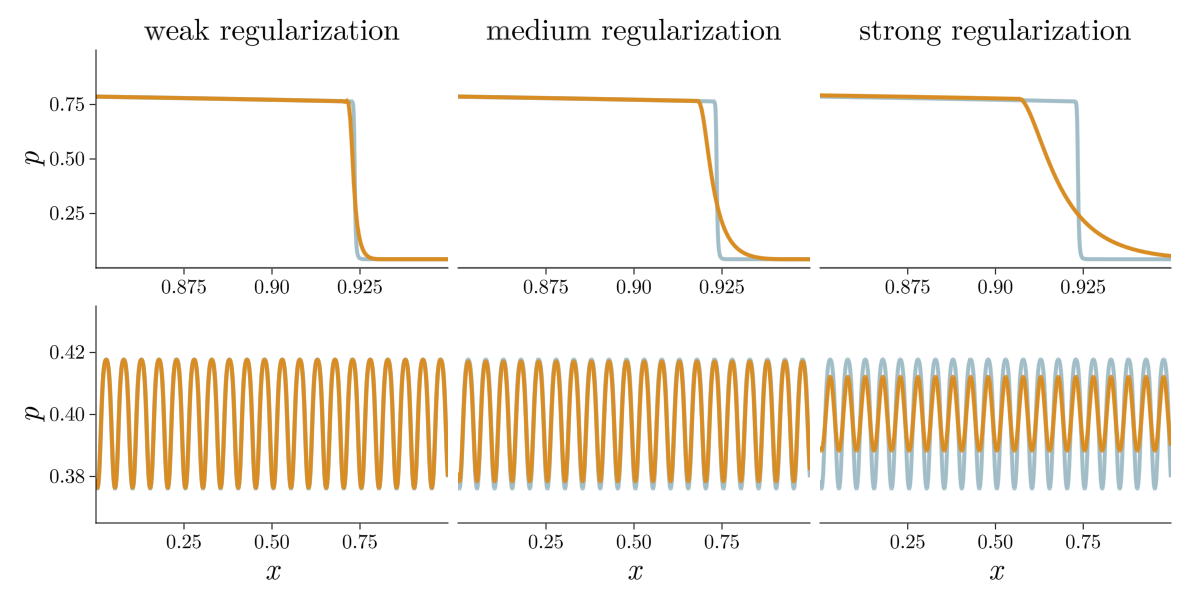
Previous approach: Viscous regularization
The field of shock capturing designs discrete or continuous models that are well-behaved on grid-resolvable scales but correctly account for the effects of the microscopic shock, without excessive energy dissipation. Explicitly or implicitly, virtually all attempts add viscosity locally near the shock to regularize it without spurious dissipation in smooth regions of the flow. This delicate balance is a major obstacle in simulating flow involving complex interactions of shock waves with physical oscillations due to acoustic or turbulent effects. The video below shows the behavior of a typical approach, on a shock and a high-frequency pressure wave, for varying regularization strengths. Weak regularization results in near-discontinuous solutions, while strong regularization damps out the sound wave. Furthermore, the shock profile’s derivative always has a near-singularity, limiting smoothness-based approximations.
Our solution: Information geometric regularization (IGR)
To overcome this challenging tradeoff, we recently proposed information geometric regularization (IGR), the first inviscid regularization. It regularizes gas dynamics without adding any viscosity. Instead, it adds to the pressure \(p\) the entropic pressure \({\color{#B8420F} \Sigma}\) defined by
\[\rho^{-1} {\color{#B8420F}\Sigma} - {\color{seagreen} \alpha} \operatorname{div}(\rho^{-1} \nabla {\color{#B8420F}\Sigma}) = {\color{#2E6B69}\alpha} \left(\operatorname{trace}^2\left([\mathrm{D} \mathbf{u}]\right) + \operatorname{trace}\left([\mathrm{D} \mathbf{u}]^2\right) \right).\]Here, \(\rho\) is the density, \(\mathbf{u}\) the velocity field, and \(\mathrm{D} \mathbf{u}\) its Jacobian. The parameter \({\color{seagreen} \alpha}\) controls the strength of the regularization. The regularized shock profiles have thickness \(\propto \sqrt{\alpha}\). The video below shows that IGR replaces shocks with smooth profiles without damping acoustic waves.
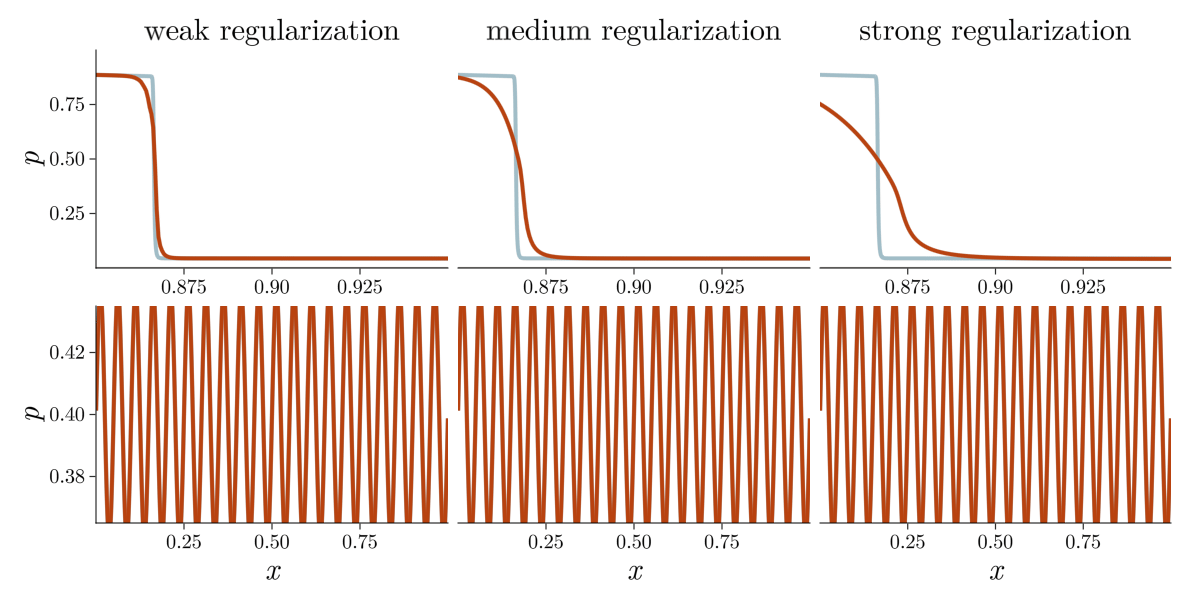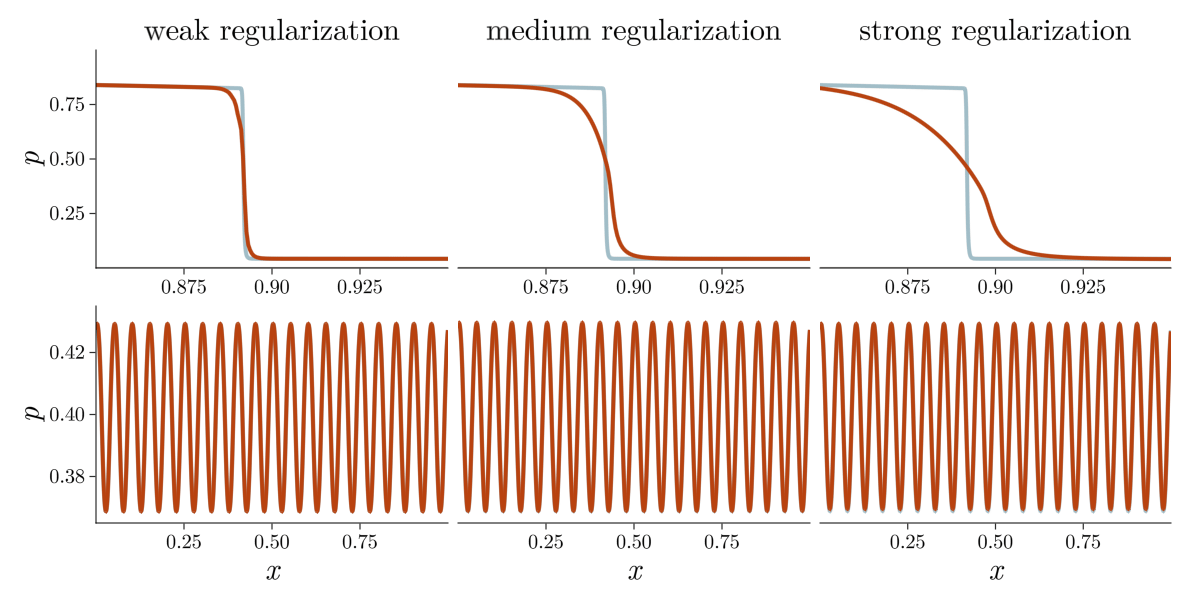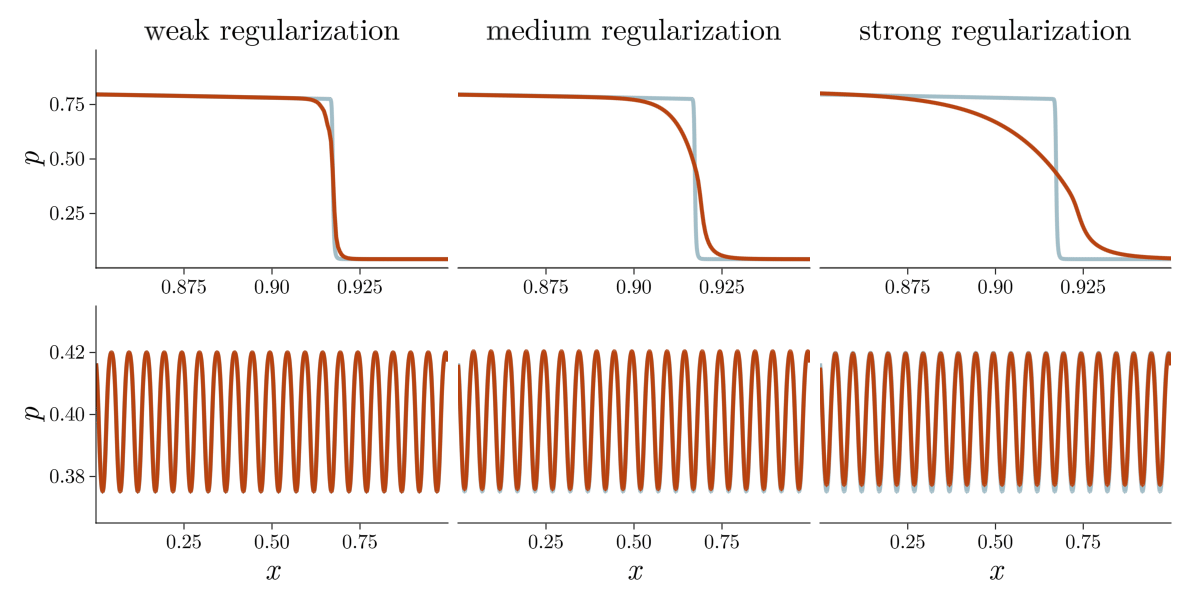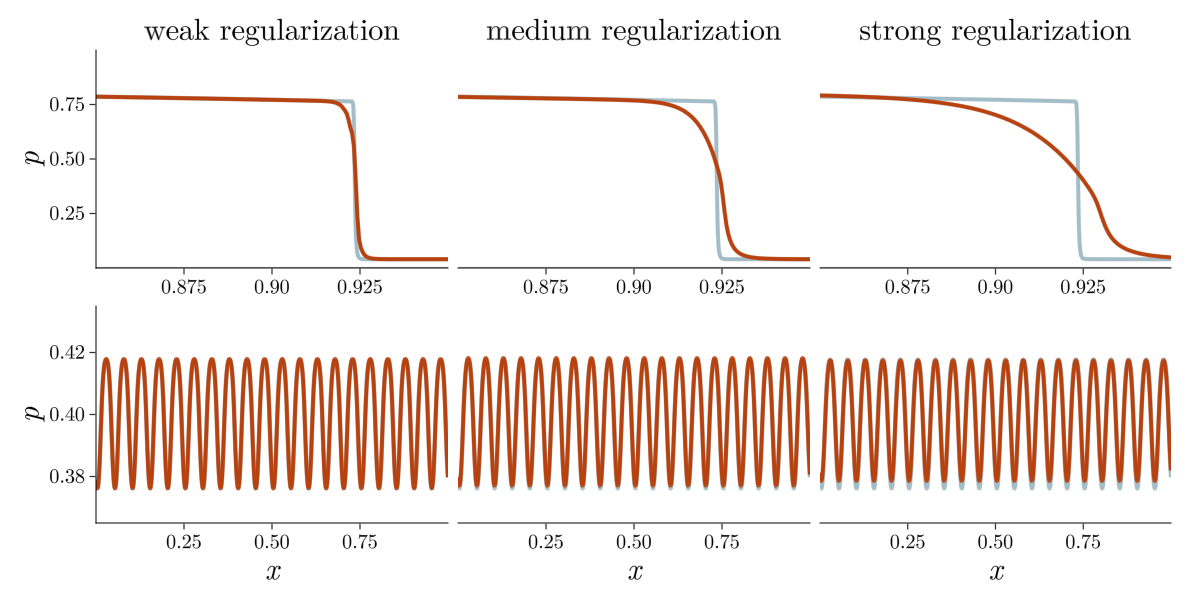
In general relativity, gravitational forces are manifestations of the curvature of spacetime. Similarly the entropic pressure \(\Sigma\) modifies the notion of straight line in the space of particle trajectories. In the modified geometry, particle trajectories merge but never cross, preventing the formation of singular shocks while maintaining nominal long-time behavior.
To explain this modification in more detail, we start with some background on shock formation.
Background: Four perspectives on shock formation
The geometry of shock formation
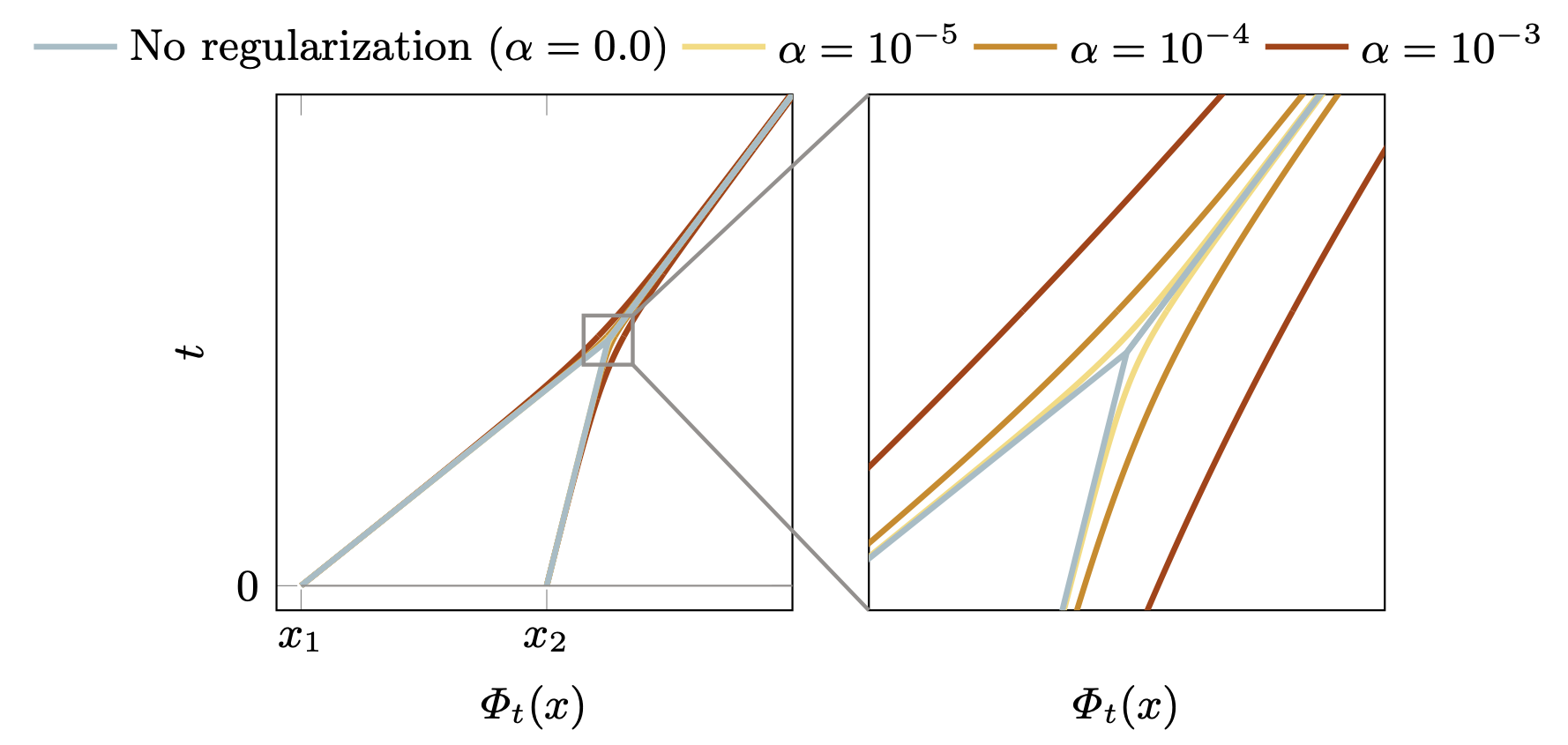
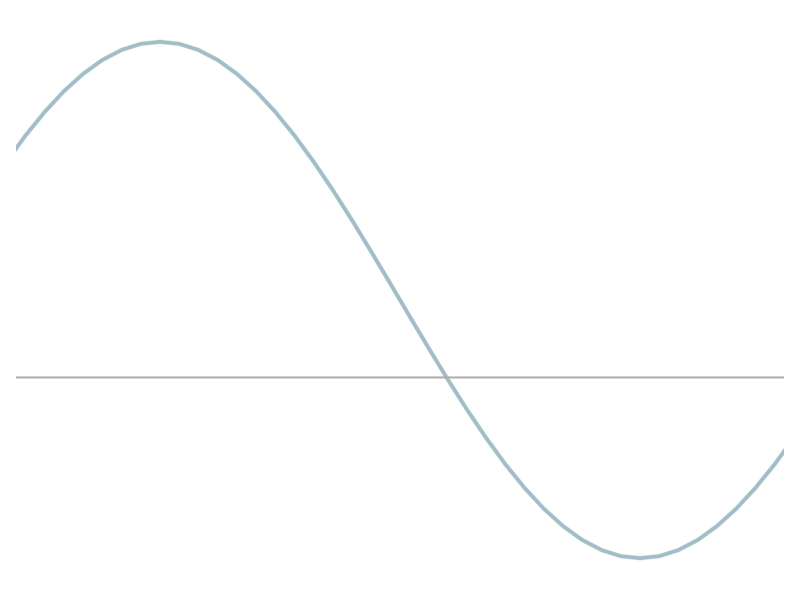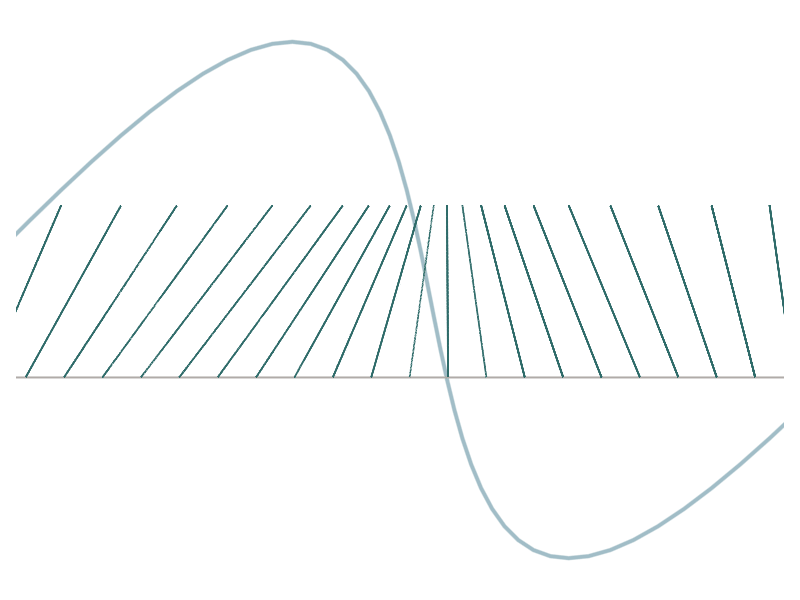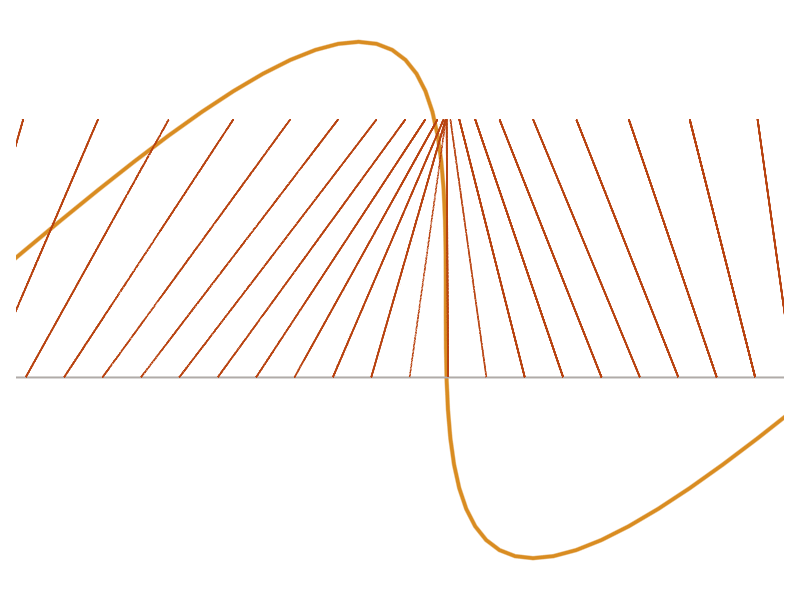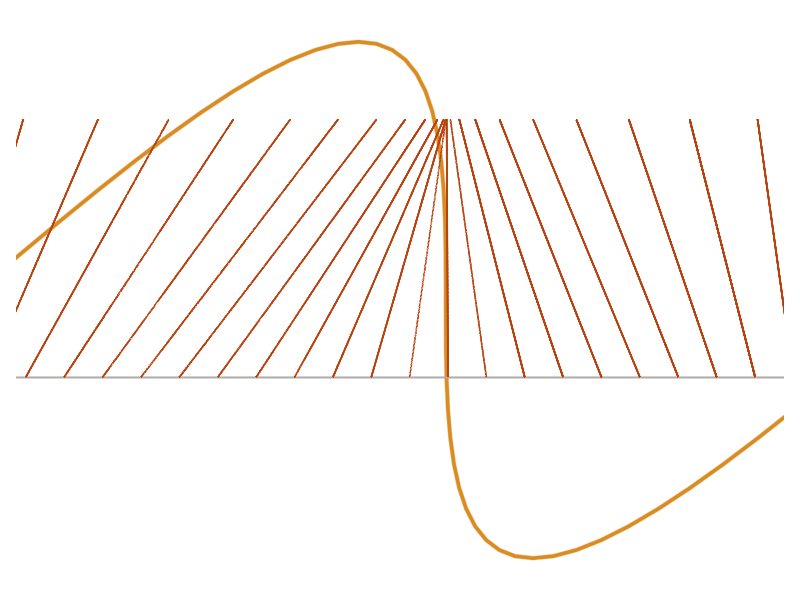
In the case of one spatial dimension and vanishing pressure, the geometry of shock formation is especially simple. Gas particles starting at \(x\) follow straight lines
\[\Phi_t\left(x\right) = x + t u_0(x),\]determined by their initial velocity. Equivalently, the deformation map \(\Phi_t\) follows a straight line \(t \mapsto \Phi_t\) in a suitable function space.
Collison of particles / with the boundary
Shocks form when gas particles collide or equivalently, \(\Phi_t\) reaches the boundary of the set of invertible functions (diffeomorphism manifold)
Collapse and constraint activation
Two lesser-known perspectives arise from mass transport and optimization. The mass density \(\rho_t\) at time \(t\) is the so-called push-forward \(\left(\Phi_t\right)_{\#} \rho_0\) of the initial density \(\rho_0\). Shocks form when the mass acumulates on individual points. The map \(\Phi_t\) also solves the minimization problem
\[\min \limits_{\partial_x \Phi \geq 0 } - t \int \limits_{\mathbb{R}} u_0(x) \left(\Phi(x) - x\right) \mathrm{d} x + \frac{1}{2}\int \limits_{\mathbb{R}} \left(\Phi(x) - x \right)^2\mathrm{d} x.\]From this perspective, shocks form when the inequality constraint becomes active.

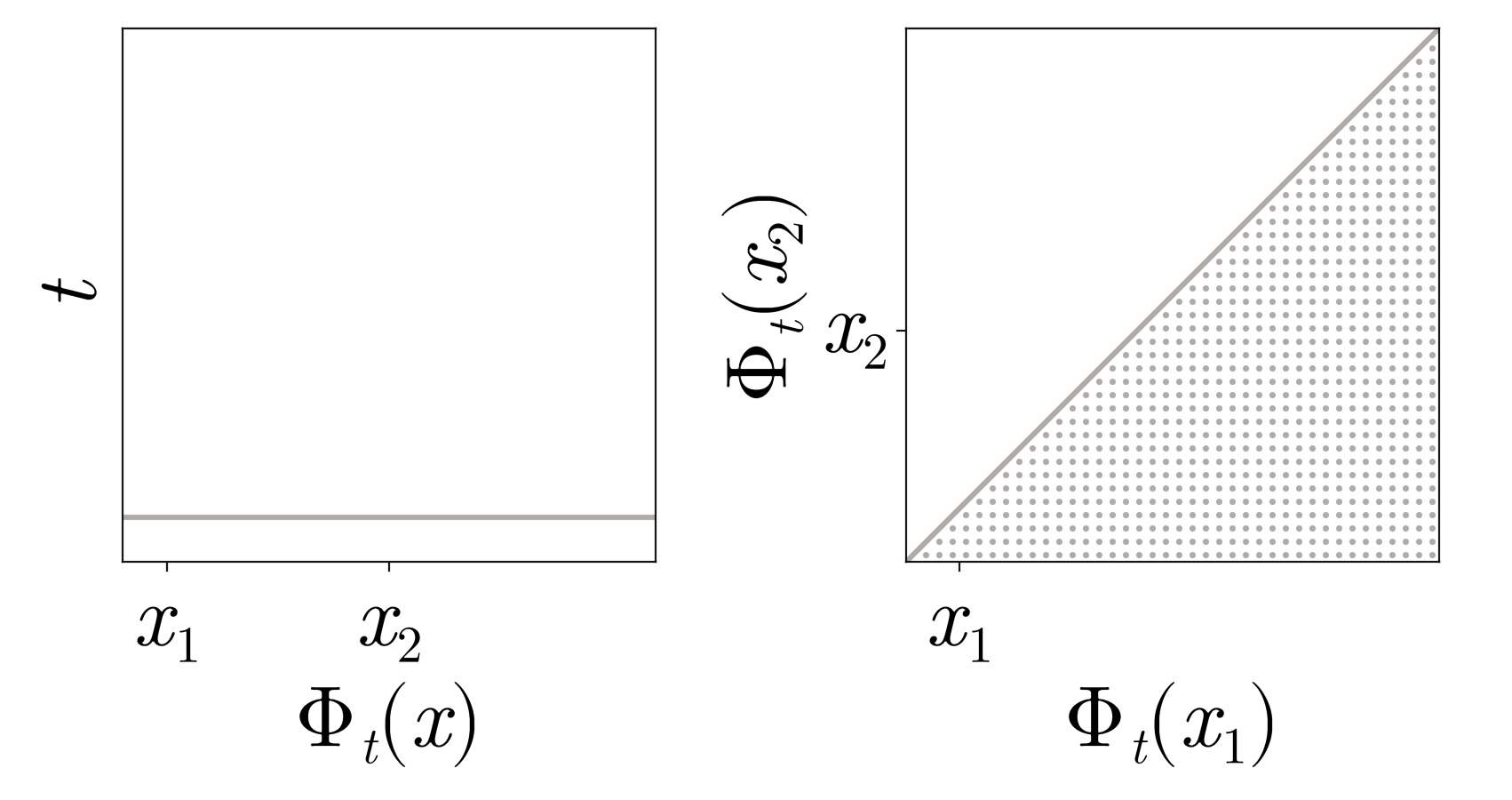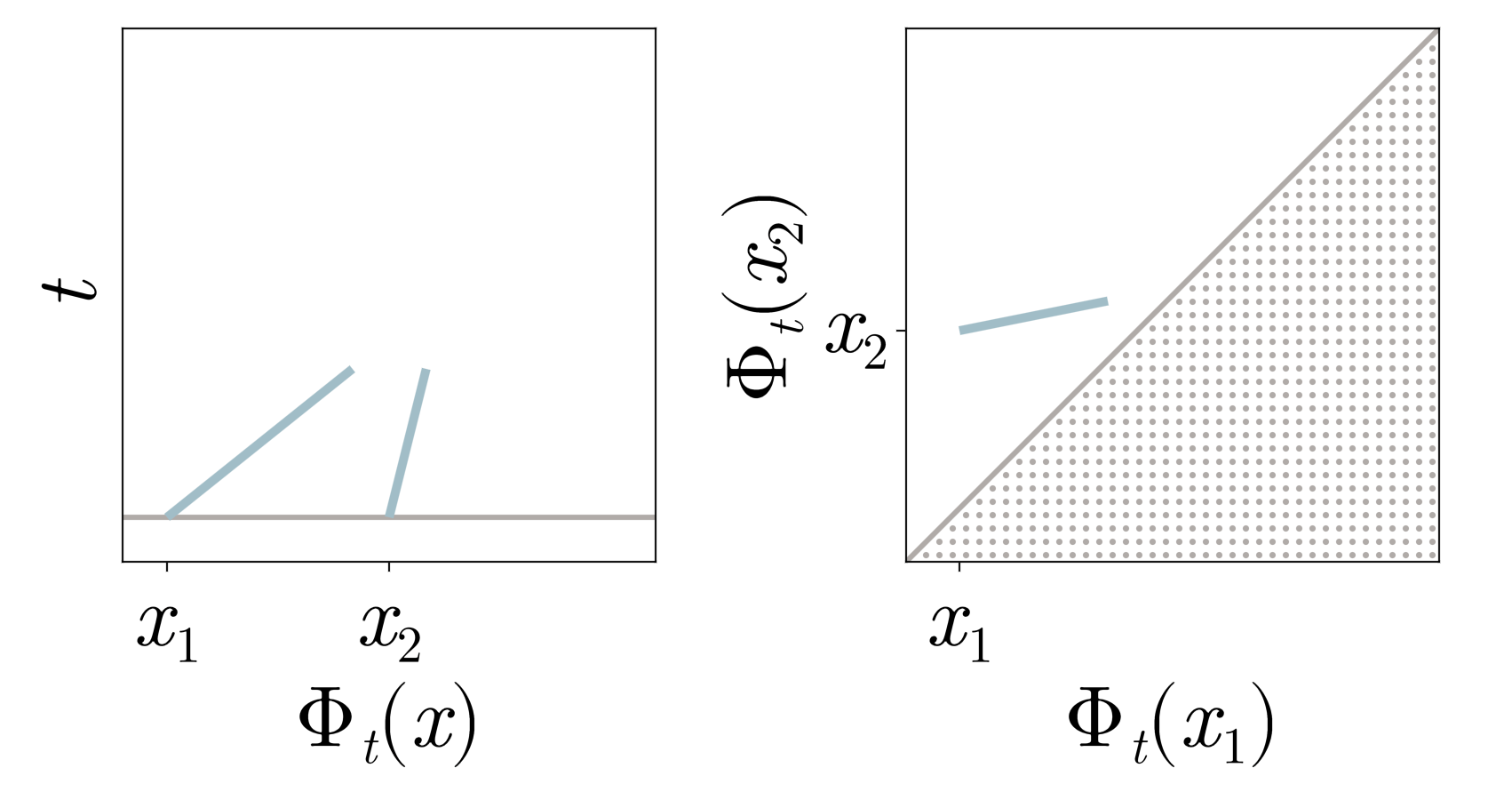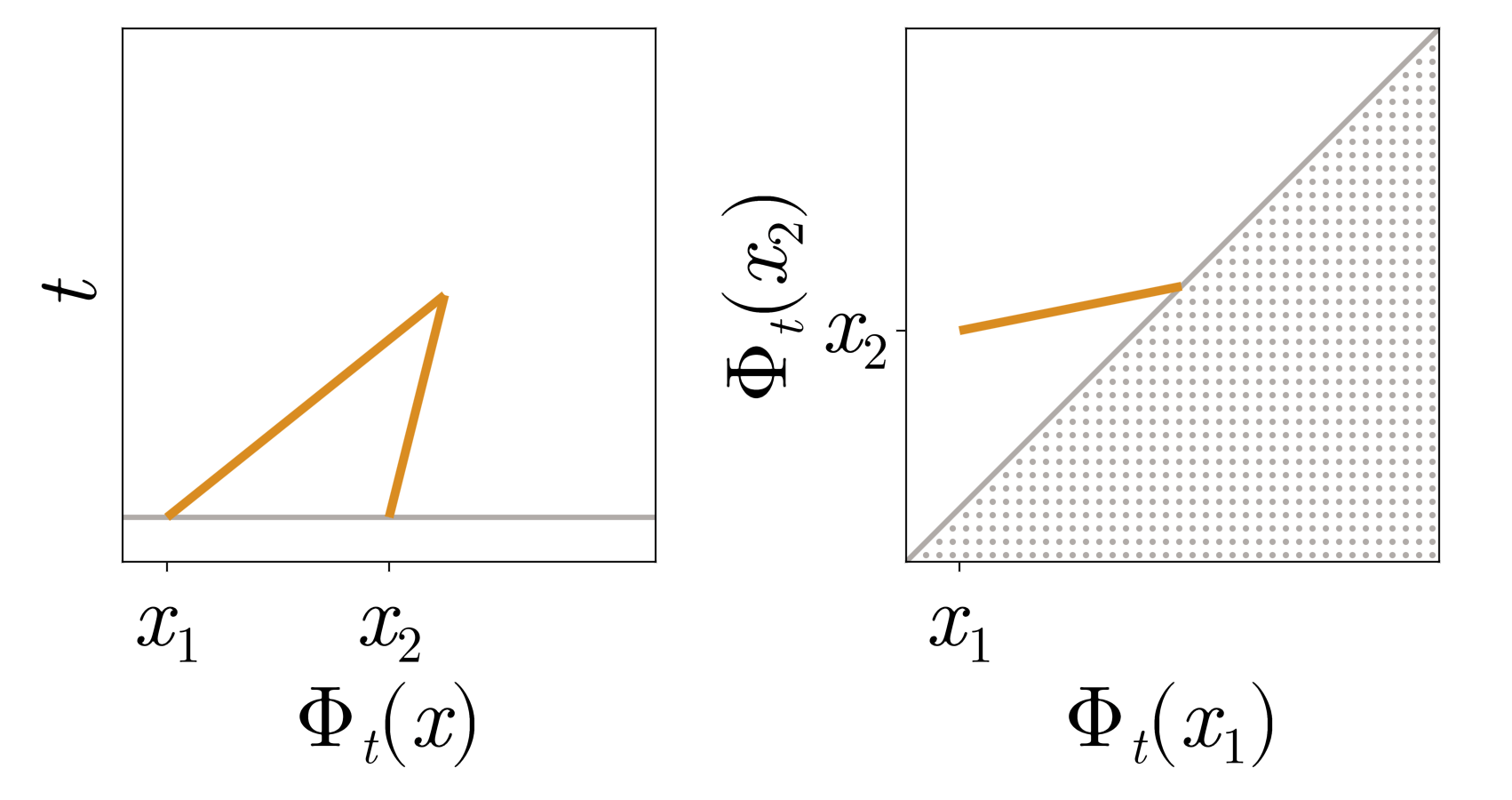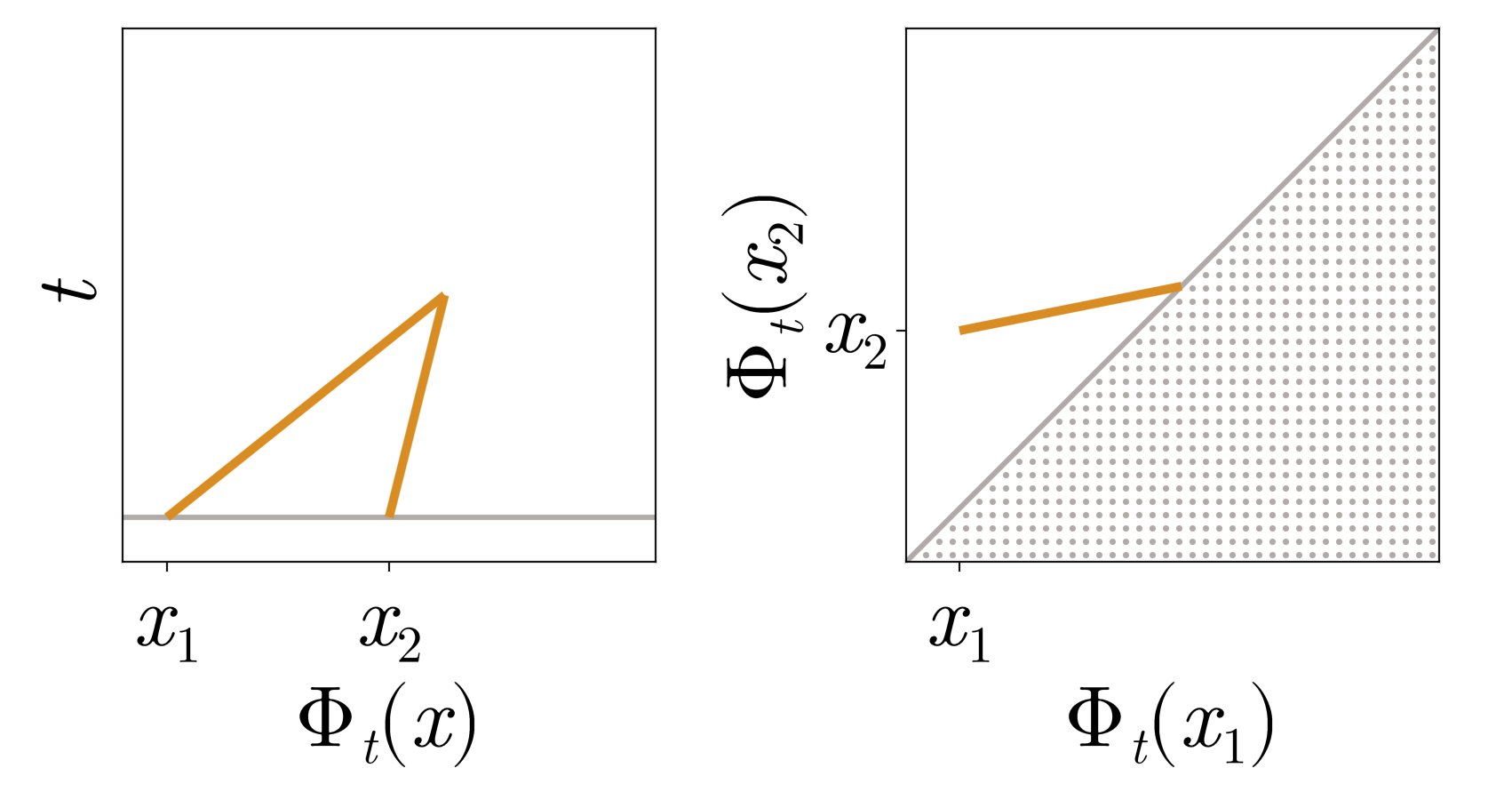
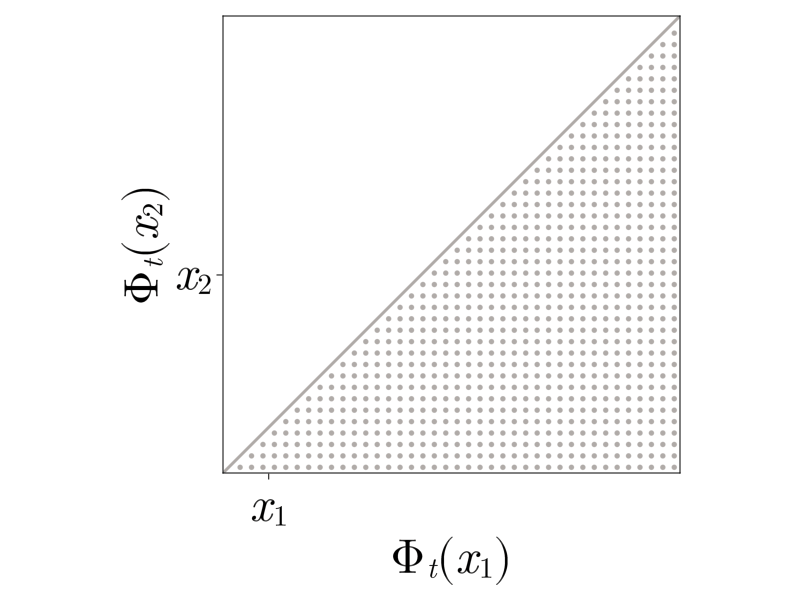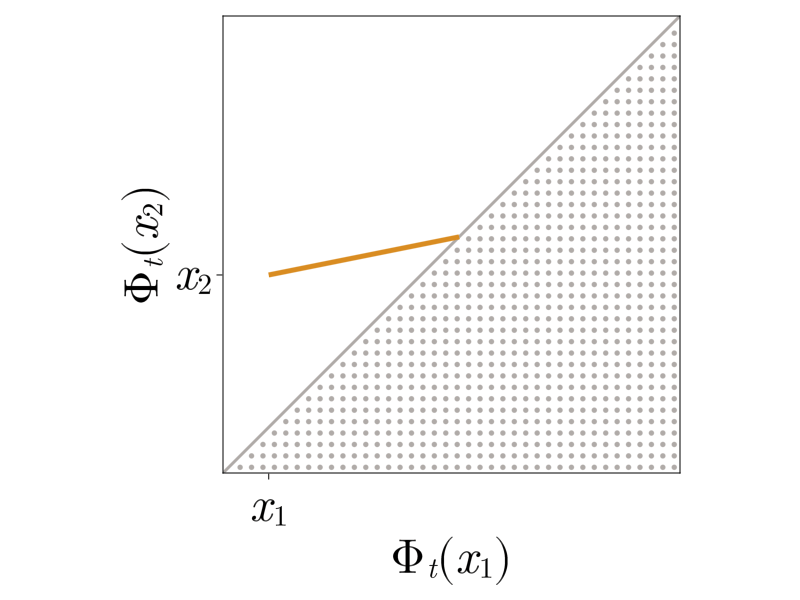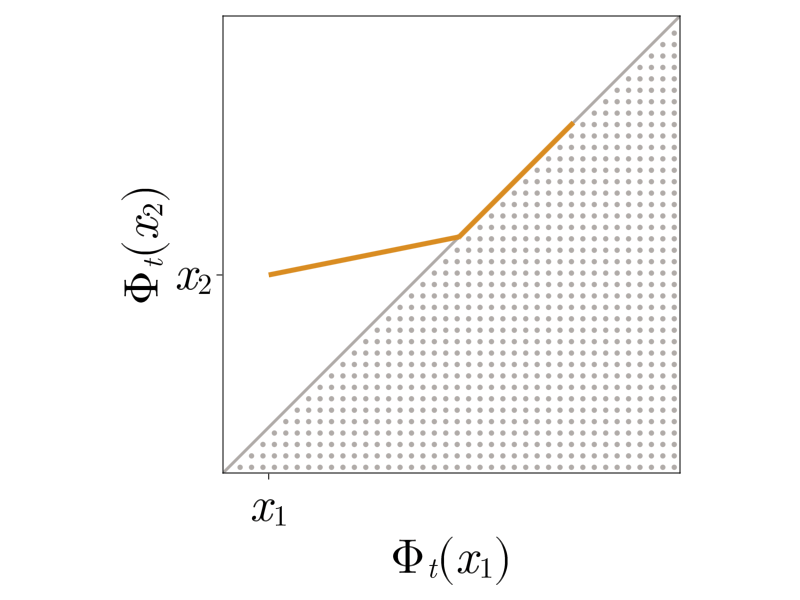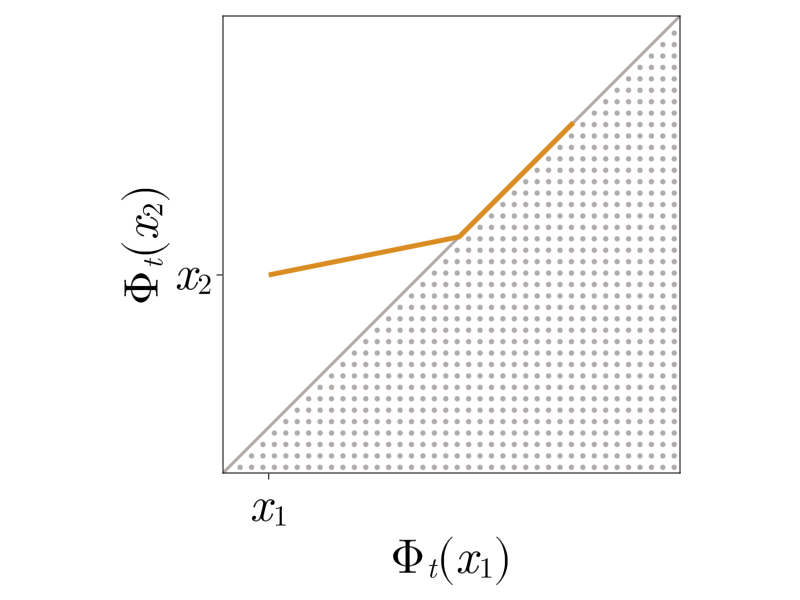
After shock
After shock formation, particle trajectories merge, \(\Phi_t\) evolves on the boundary of the set of invertible functions, propagating point masses, and satisfies the constrained problem.
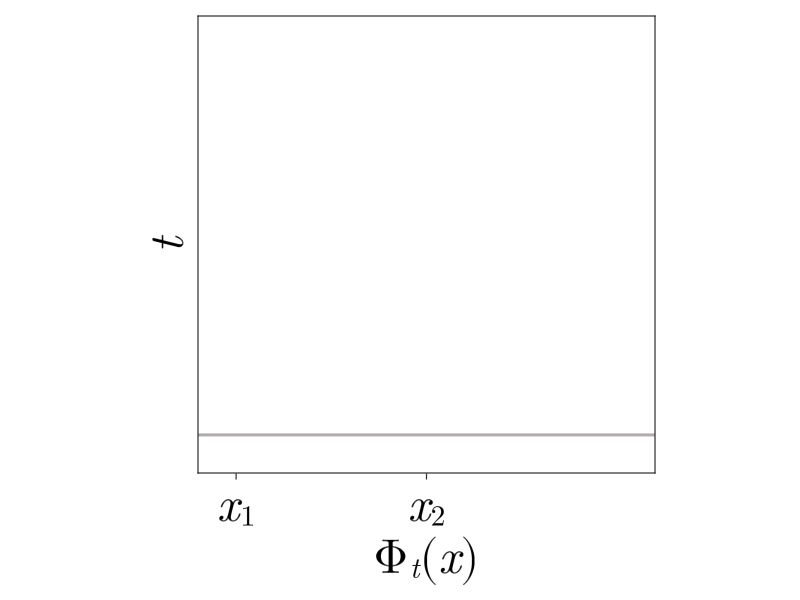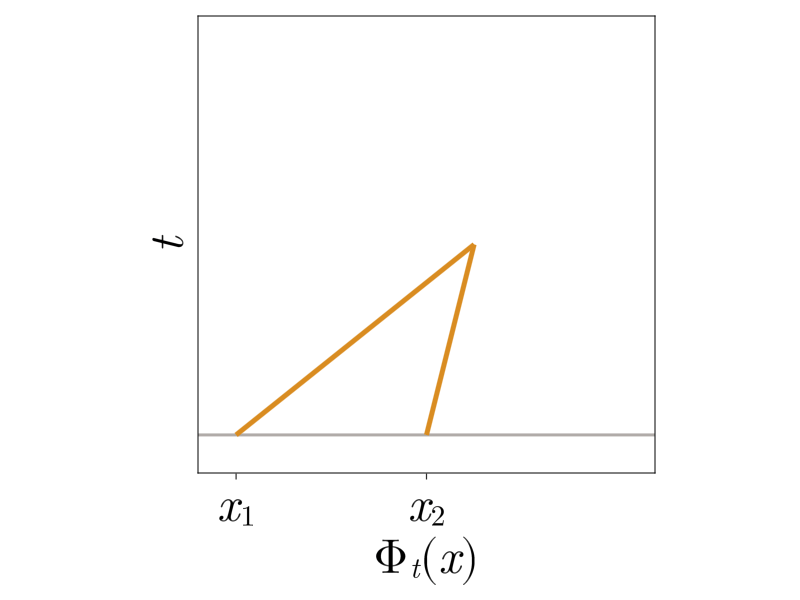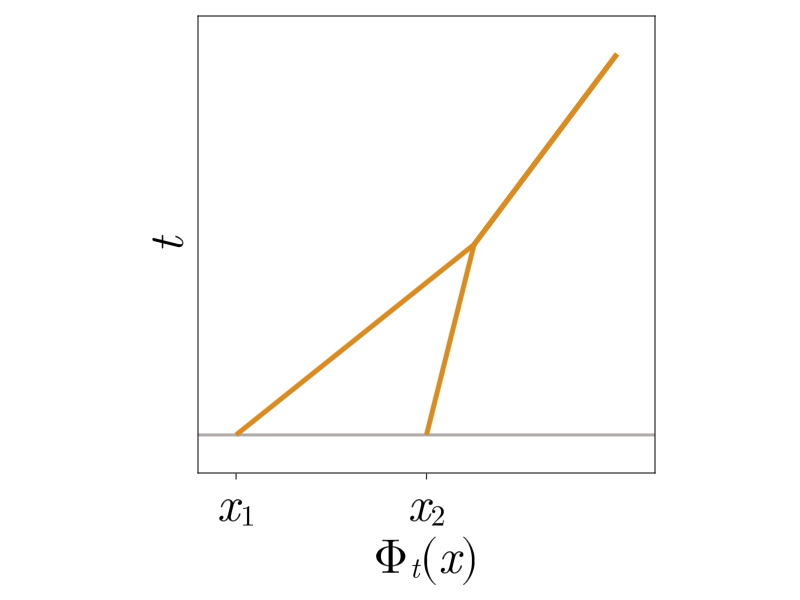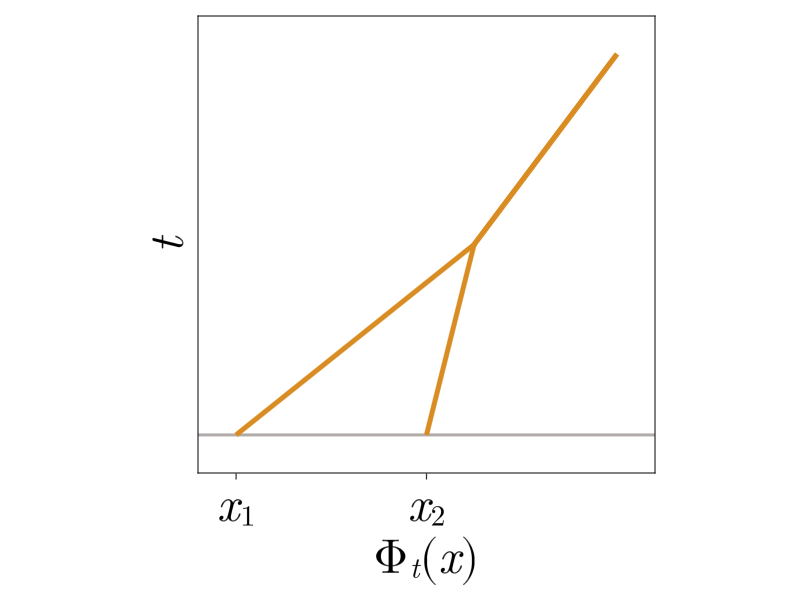

Deriving information geometric regularization
Interior point methods for fluid dynamics
The minimization definition of \(\Phi_t\) resembles so-called homotopy interior point methods. To minimize an objective, (like \(\int_{\mathbb{R}} u_0(x) \left(\Phi(x) - x\right) \mathrm{d} x\)), subject to a constraint (like \(\partial_x \Phi \geq 0\)), they add the Bregman divergence of a strictly convex function $\psi$ to regularize the problem.
\[\min \limits_{\partial_x \Phi \geq 0 } - t \int \limits_{\mathbb{R}} u_0(x) \left(\Phi(x) - x\right) \mathrm{d} x + \underbrace{ {\color{#B8420F} \psi(\Phi)} {\color{#B0ABA8} -}{\color{#B0ABA8} \psi(\mathrm{Id}) - \left[\mathrm{D}\psi(\mathrm{Id})\right] \left(\Phi - \mathrm{Id}\right)}}_{\text{Bregman divergence } \mathbb{D}\left(\Phi \; \middle\| \; \mathrm{Id}\right) \text{ of } \psi}\]As the relative weight \(t\) of the objective increases, the solution of the regularized problem converges to the minimizer of the original problem. Choosing a so-called barrier \(\Psi\) that blows up at the boundary ensures that the constraint never becomes active, greatly simplifying the solution of the regularized problems. The deformation map \(\Phi_t\) arises from choosing
\[\psi_0(\Phi) = \frac{1}{2} \int \limits_{\mathbb{R}} \left(\Phi(x)\right)^2 \mathrm{d} x.\]Shock formation thus arises from the failure of \(\psi_{0}\) to keep the regularized solution in the interior of the feasible set — the barrier is too weak! We thus regularize the barrier with a logarithmic term that blows up as we approach the boundary of the constraint set
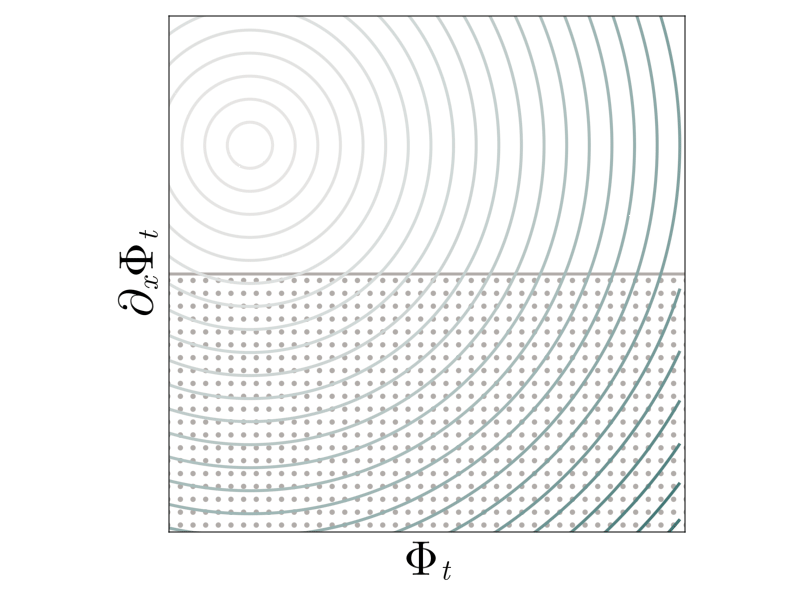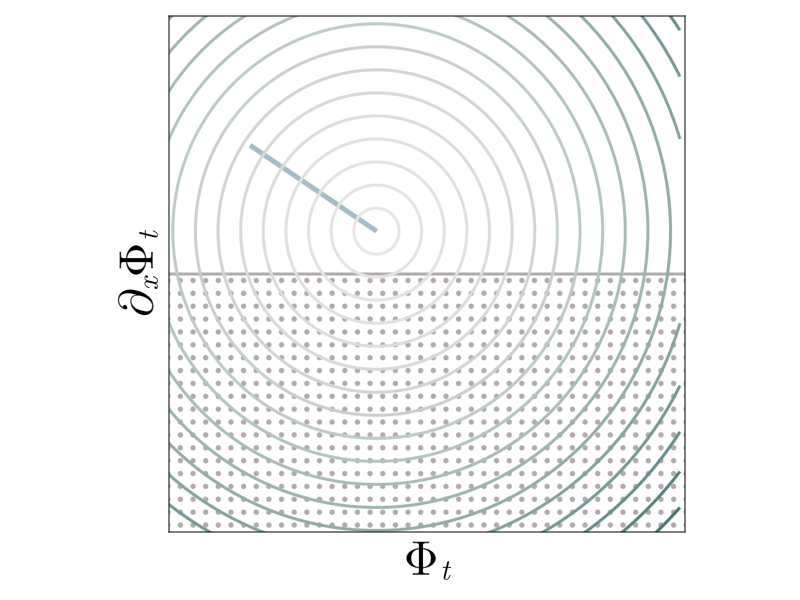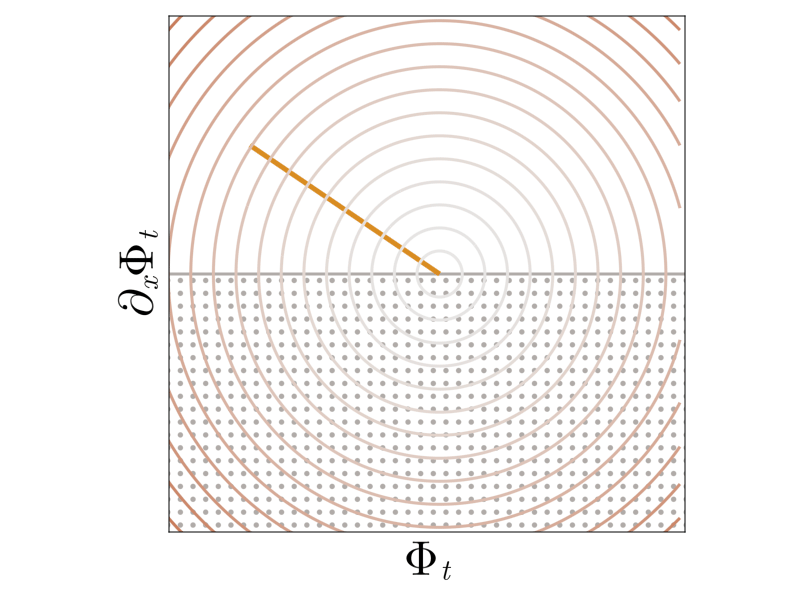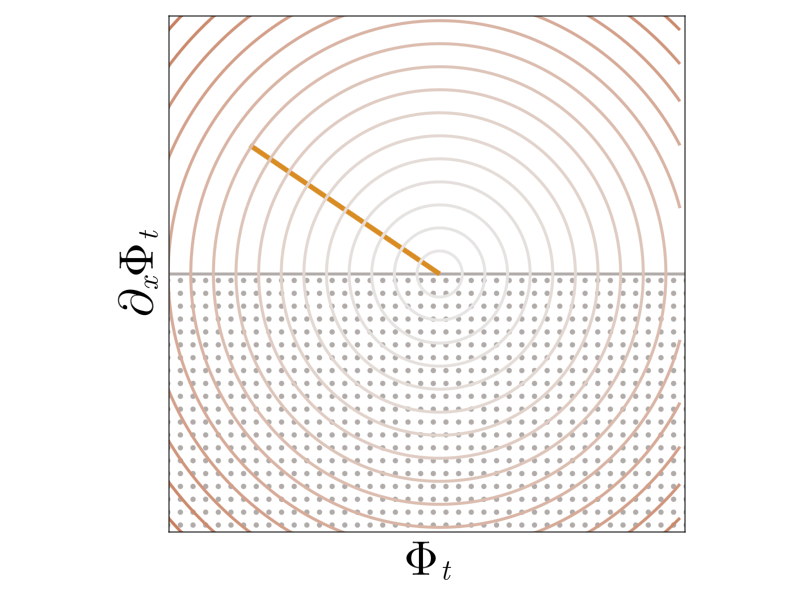
\[\psi_{\alpha}(\Phi) = \psi_0(\Phi) + \alpha \int \limits_{\mathbb{R}} - \log(\partial_x \Phi(x)) \mathrm{d} x.\]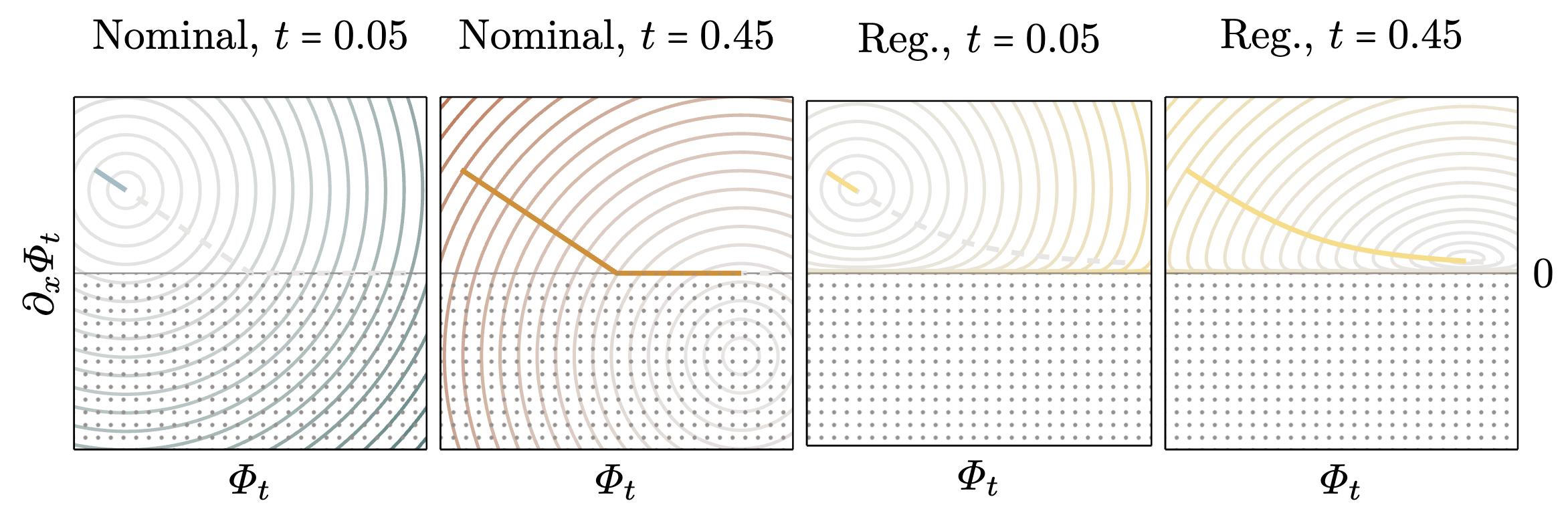
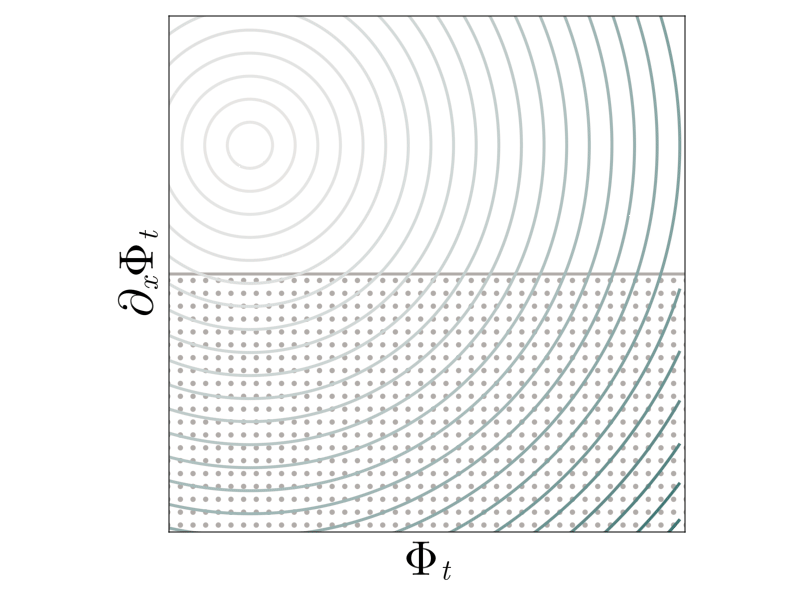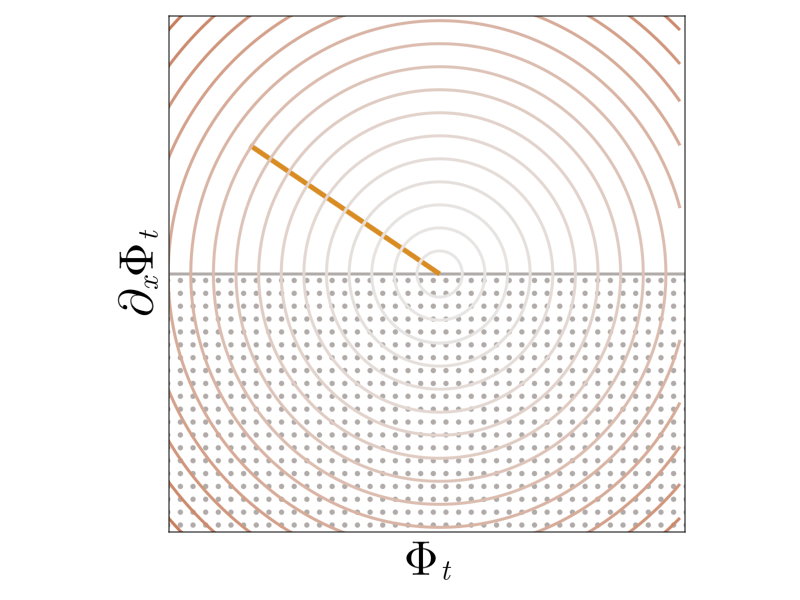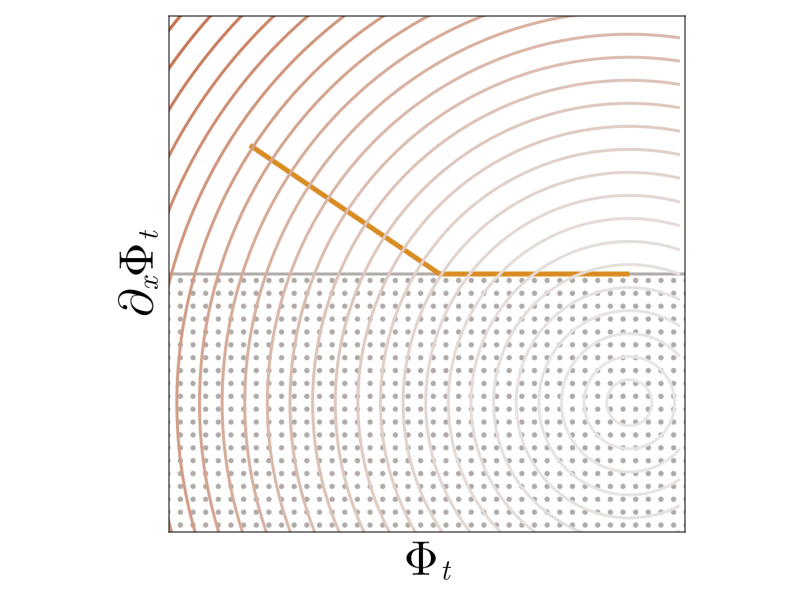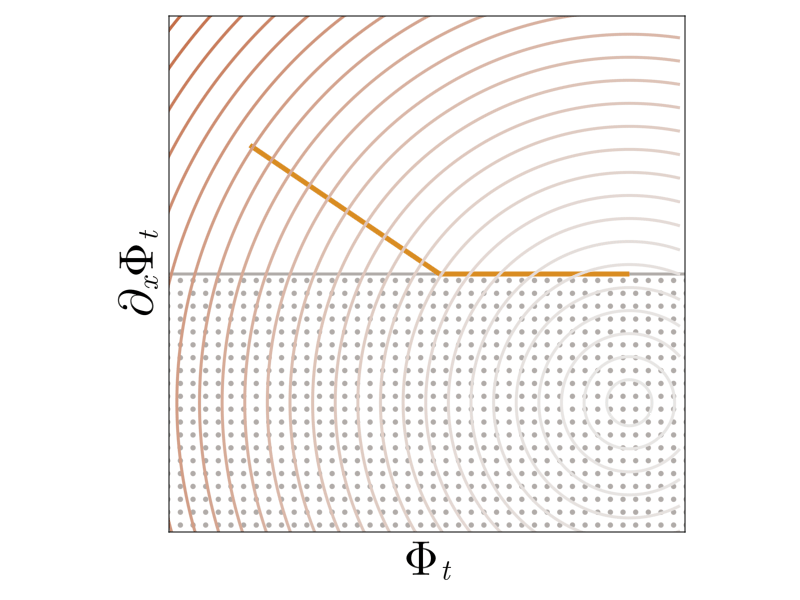
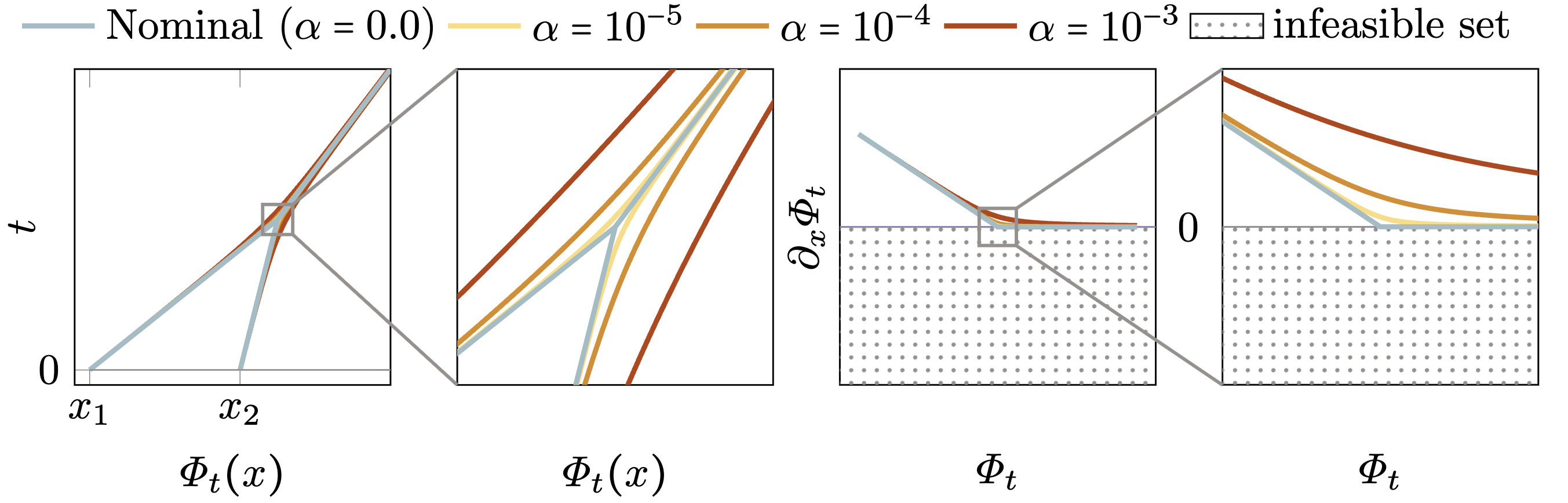
We see that with the new barrier, the solution path asymptotically approaches but never touches the boundary of the feasible set. The choice of \(\alpha\) modulates the strength of the regularization. Larger \(\alpha\) yield more boundary-avoiding behavior, but for all choices of \(\alpha\) the asymptotic behavior is the same as the nominal solution.
Expressing the minimizers as particle trajectories, we see that in the modified trajectories particles approach each other without touching. This avoids formation of singular shocks while maintaining the nominal long-time behavior!
From barriers to geodesics
The minimization form of \(\Phi_t\) is highly specific to the unidimensional pressureless case. To obtain a general approach we take a differential geometric perspective. The key idea of differential geometry is to distinguish between points \(p \in \mathcal{M}\) on a manifold and infinitesimal directions of displacement living in their tangent space \(T_{p}\mathcal{M}\). These two objects are connected by the exponential map \((p, v) \mapsto \operatorname{Exp}_{p}(v)\) that returns the destination reached by traveling from \(p\) in the direction of \(v \in T_{p} \mathcal{M}\). Linear algebra uses the Euclidean exponential map \(\operatorname{Exp}_{p}(v) := p + v\), but in general there are numerous ways to define “traveling on a straigth line in an initial direction”. A strictly convex barrier function defines a so-called dual exponential map \(\operatorname{Exp}^{\psi}_{(\cdot)}\left(\cdot\right)\) as the Euclidean exponential map in the space of gradients of \(\psi\). The resulting straight lines of the form \(t \mapsto \operatorname{Exp}^{\psi}_{p}\left(t v\right)\) are called dual geodesics.
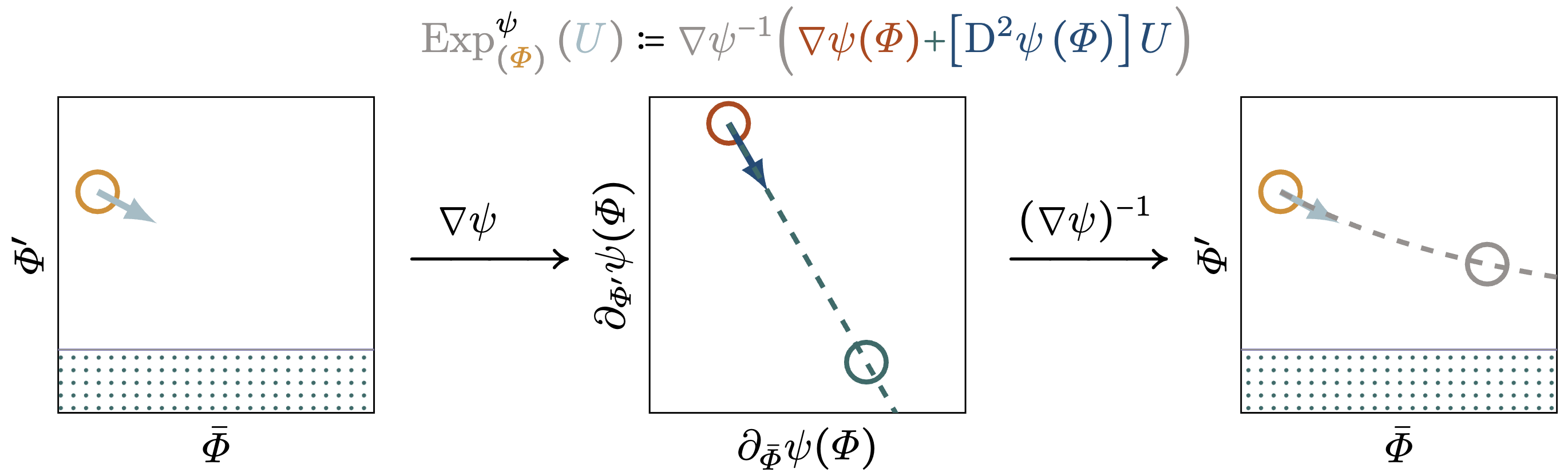
Crucially for our purposes, the minimizing paths \(\Phi_t\) of the last section are dual geodesics generated by \(\psi_{\alpha}\). This generalizing our regularization beyond the unidimensional pressureless case by replacing particle trajectories with dual geodesics.
Information geometric regularization and information geometric mechanics
After deriving modified differential equations for \(\Phi\), we can recover the resulting velocity \(\mathbf{u}\) and density \(\rho\), yielding a modifed conservation law with \(\Sigma\) added to the pressure. The regularization term \(\int_{\mathbb{R}} - \log(\partial_x \Phi(x)) \mathrm{d} x\) is equal to the negative Shannon entropy \(\int_{\mathbb{R}} \log(\rho) \rho \mathrm{d} x\) of the mass density. In fact, its dual geodesics are the only notions of straight line that continue indefinitely (geodeiscally completen), are Euclidean in the right coordinate system (flat), and are invariant under sufficient statistics of the density (Markov invariant). Information geometric regularization augments the Euclidean geometry of individual particles with the information geometry of particle distributions. It thus accounts for the dual nature of $\rho$ as being a statistical estimate of physical particles.
IGR in practice
Shock capturing without viscosity and limiters
In practice, information geometric regularization allows dispensing with sophisticated shock capturing approaches of the path and instead deploy high-order linear numerics to the regularized equation. For instance, we can take a finite volume method with fifth-order accurate WENO reconstruction and remove the WENO limiter, using just the fifth order reconstruction applicable to smooth functions. The inviscid nature of IGR allows capturing subtle fine-scale features even when using relatively coarse meshes, whereas the WENO limiter diffuses them.
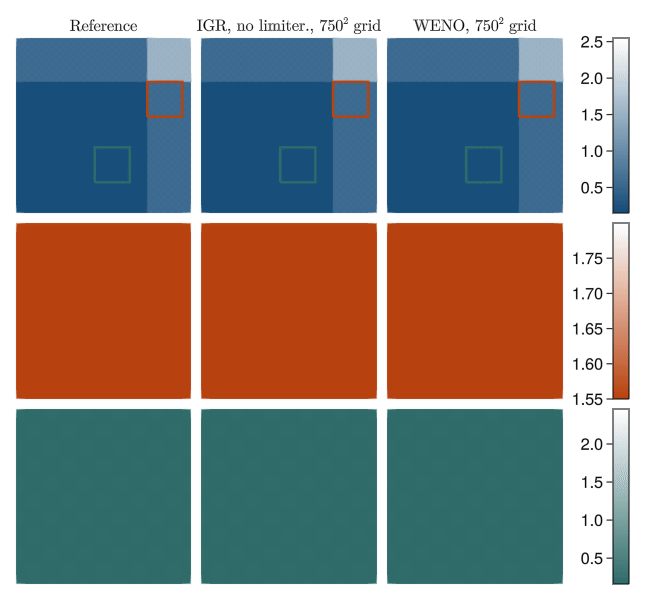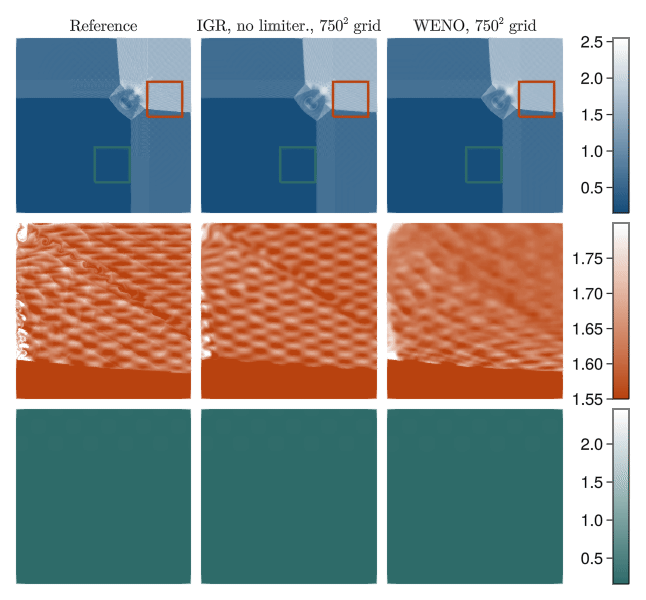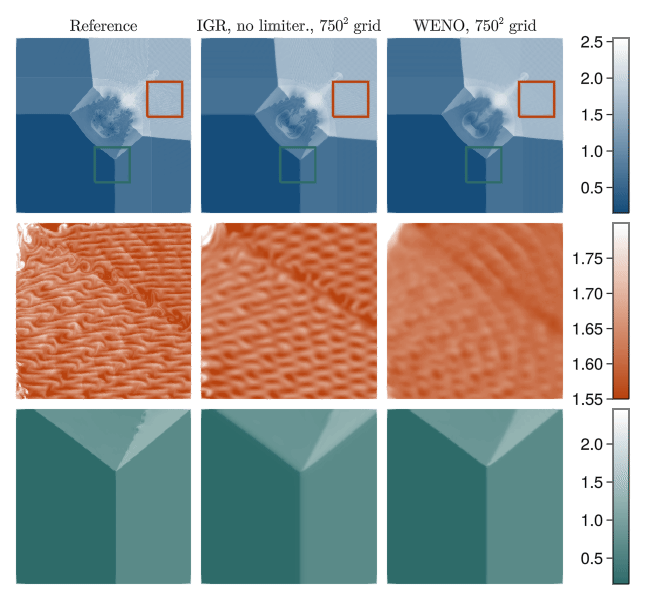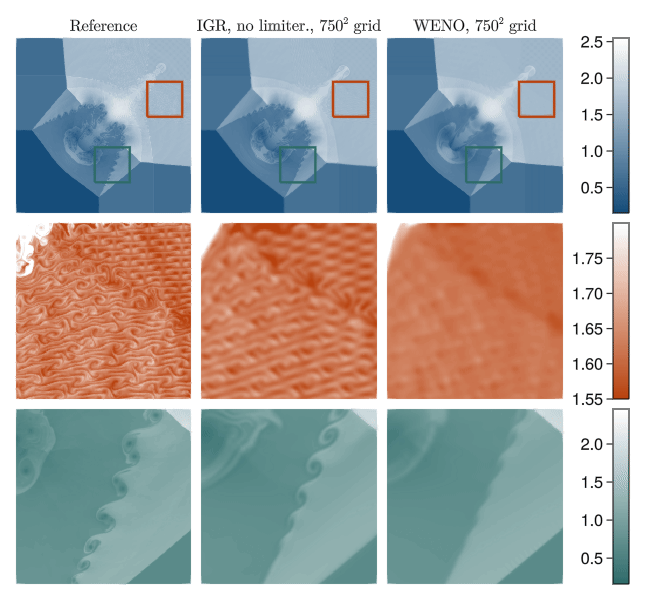
IGR at scale
To conclude, I want to point out that IGR is readily applicable to large, three dimensional problems. In recent joint work with Benjamin Willfong, Anand Radhakrishnan, Henry Le Berre, Nikolaos Tselepidis, Benedikt Dorschner, Reuben Budiardja, Brian Cornille, Stephen Abbott, and Spencer Bryngelson we integrated IGR into the exascale-ready MFC Code to conduct the first-ever compressible finite volume simulation with more than 100 trillion grid points! IGR played a key role in this endeavor by simplifying shock treatment, and thus the overall numerics.